ACES2065-1 to ACEScg negative value issue question?

[Troy_James_Sobotka (troy_s)]

@Thomas_Mansencal

I was thinking about this some more and concluded that rendering in the Camera Gamut doesn’t necessarily minimises the error compared to spectrally render using the camera primaries.

Perhaps it is worth considering the implicit ideology of “error”. What metric? Why? What else is there that is implicit in the idea around “error”?

I would suggest that within “rendering”, there’s a certain blind energy conservation at work. The idea of energy conservation might be worth exploring.

For example, the silicon number cruncher doesn’t care what the sub-bands are of the filtration employed in a sensor, as we know the quantal catch correlates with the integral of the summed wattage per frequency band.

Are we certain that there’s energy conservation from a quantal catch to colourimetry? Does it matter? Is this considered in our discussions around “error”? How does a difference in energy levels in the three bands of colourimetry impact the resulting colourimetry under additively exponential and multiplicatively exponential basic interactions?

[Derek]

If the goal was integrating CG with camera footage would the workflow be to set the working space of Nuke to linear camera space and convert the render from ACEScg into that camera working space?

I imagine rendering in the camera space would be problematic, for similar reasons to those that were the impetus for creating AP1 for rendering CG rather than AP0. Is that correct? By render I do not mean a spectral render, but rather a render like Arnold or Renderman.

[Thomas_Mansencal]

@Troy_James_Sobotka

Perhaps it is worth considering the implicit ideology of “error”. What metric? Why? What else is there that is implicit in the idea around “error”?

The metric we used was always a simple RMSE, nothing perceptual to avoid bias or preference. It is akin to a measure of energy imbalance between the two methods.

[Troy_James_Sobotka (troy_s)]

@Thomas_Mansencal

The metric we used was always a simple RMSE, nothing perceptual to avoid bias or preference. It is akin to a measure of energy imbalance between the two methods.

This is a tautological statement.

If our question is about “error”, it is always enmeshed in the basis projection and the unit of metric.

Therefore, taking the Root Mean Squared is simply taking the square root of the mean square of the metric in question, which begs the question we are trying to answer.

If we consider that the CIE XYZ basis vectors are in scaled units of luminance, and that the luminance is uniform with respect to relative units of wattage, we can see an analysis point emerge. For every one unit of relative wattage input, are we sure that our colourimetric transformations maintain a relative energy invariance?

It is possible to show that the answer to this is “No”, and that there are implicit cognitive problems with the approach. A good example would be the sunset picture that @chuckyboilo showcased in the other thread.

Here is the OpenDRT rendering from @jedsmith which showcases a peculiar “lustre” in the interior of the “sunset” pictorial depiction. If we examine the sample line of the relative wattages down the right side, we can see that the interior of the sunset is at a lower relative wattage to the peripheral gradations, where the left side is lower relative wattage, and the right side is higher. The vertical spatial depiction is correlated with the graph “height”.

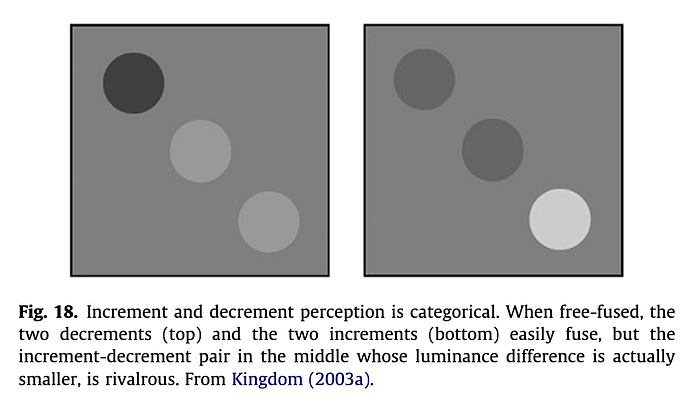
We know that the increment to decrement signals are categorical; the increment and decrement signals flow from the retinal assembly as two unique and distinct gradient signals, and are not integrated. Kingdom¹ demonstrates this rather elegantly using a haploscopic fusion approach, and the “lustre” that emerges.

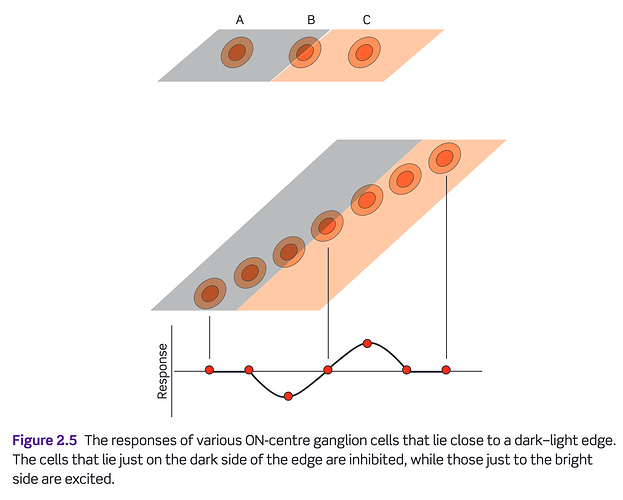
We can realize that the signal gradient strength is directly correlated to the electromagnetic radiation via transduction. “Derp up energy” and “derp down energy” as per the following diagram², which illustrates a single constellation of an ON-centre cell, which has a sibling in the OFF-centre, and is the origin of the increment (ON-centre) and decrement (OFF-centre) signals themselves. We should remember there are three flavours of these twin ON and OFF identities, one of which can be loosely considered “luminance”:

Given that we know that luminance increments and decrements hold a privileged role in the visual system, we can see from the second picture that a luminance analysis of the stimuli from the picture is equi-luminant. The source of the peculiar “lustre” does not appear to be induced by a luminance polarity reversal:

If we look to the first picture with its corresponding plot, we can see that the basic colourimetric transformation has led to a cognitively dissonant “spreading” of the relative wattages such that the sensor quantal catch clipped region, would implicitly correlate to the highest quantal catch of the entire buffer; literally all other quantal catches would have been lower than this region.

A generic first stage “white balance”, using three coefficients would not change this relationship as an aside. Multiplying each plane by a varying coefficient would always yield the photosite saturated region as the highest energy relative to all other coordinates.

It follows that if one subscribes to a peculiar “lustre” in the formed picture, and we have some idea of the audit trail of OpenDRT to know that Mr. Smith’s effort does not rely on any relative wattage deforming functions, we can rule out the error as being a byproduct of the algorithmic approach they have chosen. This forces us to ask the question as to where this cognitively dissonant relative wattage error being introduced and why?

I believe a reasonable mind should be able to verify that the most basic colourimetric 3x3 leads to an energy invariance, which would have considerable influence on a visual system that is entirely oriented around increment to decrement signals.

All of this is completely moot if someone believes everything is all well and good in the formed picture. Go forth and prosper.

–

¹ Kingdom FAA. Lightness, brightness and transparency: A quarter century of new ideas, captivating demonstrations and unrelenting controversy. Vision Research. 2011;51(7):652-673. doi:10.1016/j.visres.2010.09.012

² Snowden RJ, Thompson P, Troscianko T. Basic vision: an introduction to visual perception. Rev. ed. Oxford University Press; 2011.

[Thomas_Mansencal]

@Troy_James_Sobotka

Therefore, taking the Root Mean Squared is simply taking the square root of the mean square of the metric in question, which begs the question we are trying to answer.

Talk about tautology

RMSE is THE metric by which we measure the error.

[Troy_James_Sobotka (troy_s)]

@Thomas_Mansencal

Talk about tautology

RMSE is THE metric by which we measure the error.

That’s actually a metric, disconnected from the meaning of “error”. What is it quantifying?

If indeed there is an error of energy relationships, is it revealing details about the energy relationships? No.

If the error is in CIE XYZ trichromatic units, then the units can be related to the input wattages by way of integration. It would seem reasonable that the sign of an “error” is plausibly of significant importance.

But no, my statement was not tautological. Must be a language barrier.

[Thomas_Mansencal]

@Troy_James_Sobotka

But no, my statement was not tautological. Must be a language barrier.

[KevinJW (Kevin Wheatley)]

I took from the conversation the question of if RMS has a metric associated with it, to which the answer is that RMS is still measured in the signal’s original metric, So you can’t compare RMS of one thing with another directly, without some form of interchange,

RMSE of house prices in £ gives an error in £
RMSE of house prices in $ gives an error in $

You still need to convert £<->$ to compare/equate them.

[Troy_James_Sobotka (troy_s)]

Let me get this right…

1. I point out that saying “The metric we used was always a simple RMSE” is tautological.
2. A catastrophic failure of decoded communication occurs, and then, in place of employing meatware biological cognition, a screenshot of ocean boiling Assembled Statistical Slop software output is employed to regurgitate the idea that seems to statistically string together a series of words that an RMSE is a tautological, non statement of error metric.

Kevin, on the other hand, used the biological meatburger, and appears to have properly decoded the communication; the point that the numerical metric holds no meaning unto itself. The number is a rather low utility value that is a Euclidean distance metric of some implicit model structure. It is not applicable to the problem conjecture along some assumed veridical metric of Universally Interchangeable Truthiness.

—

If the goal is to identify a “unit of error”, then the number has to be framed relative to the problem space. I was stating that the definition of the problem space is ill defined.

In this case, here is the falsifiable conjecture:

1. That increment and decrement stimuli are cognizable to human primates. In an A to B picture arrangement, an increment in one region changed to a decrement is deleterious to the stimuli arrangement, and detectable.
2. That CIE based colourimetric 3x3 transforms create a relative wattage lack of conservation that directly leads to these increment to decrement polarity swings.

The goal would then be to formulate a metric of error that can falsify this conjecture. This should be viable given that the RGB linear values are a straight line to relative wattages. Following the conjecture, any error metric would likely be required to:

1. Show that no such relative energy discrepancy exists. If a relative energy discrepancy does exist then:
2. Show that the error does not result in an increment to decrement polarity shift in identical arrangements of stimuli expressed in two different colourimetrically defined spaces. This would imply that said metric should include a sign of gradient to distinguish an ascending slope from a descending.

The other option is to go about their day dreaming about glazed donuts.

[Thomas_Mansencal]

@KevinJW

You still need to convert £<->$ to compare/equate them.

Indeed, and, the interchange has occurred, the metric is applied to the computed samples upon their conversion to the same RGB colourspace.

For other readers and give more context: We are effectively quantifying an energy conservation issue between computations happening in the radiometric domain and computations occurring in the photometric domain. The RMSE metric is applied in the photometric domain on the set of samples. We can then rank different RGB colourspaces and find one, or a group of them, that exhibits a reduced RMSE value.

@Troy_James_Sobotka

I point out that saying “The metric we used was always a simple RMSE” is tautological.

But it is not! I’m asserting which metric was used, that it was RMSE, and that we consistently used that metric. There’s no circularity or logical necessity in the statement.

[ChrisBrejon (Christophe Brejon)]

@Finn_Jager

→ ACES viewtransforms/DRTs quiet frankly are not up to snuff so every show rolls their own anyhow. Never found a single DP that liked the image formation, even 2.0 and I am sorry to say this but its just not good.

Is there any way for you to describe this more precisely ? I think that would be helpful. Especially regarding the ACES 2.0 Output Transforms.

Thanks !

[Troy_James_Sobotka (troy_s)]

@Thomas_Mansencal

But it is not! I’m asserting which metric was used, that it was RMSE, and that we consistently used that metric. There’s no circularity or logical necessity in the statement.

RMSE is a mean “length” along some metric, and does not describe the units of metric unto itself, nor is there necessarily utility in said “length”.