Thanks @ChrisBrejon! Now that you’ve made this excellent diagram explaining everything, I reworked the parameters a bit to hopefully make it more clear what is going on. I realized after reading my post again with a fresh brain that there were some things that could be made more clear and simplified.
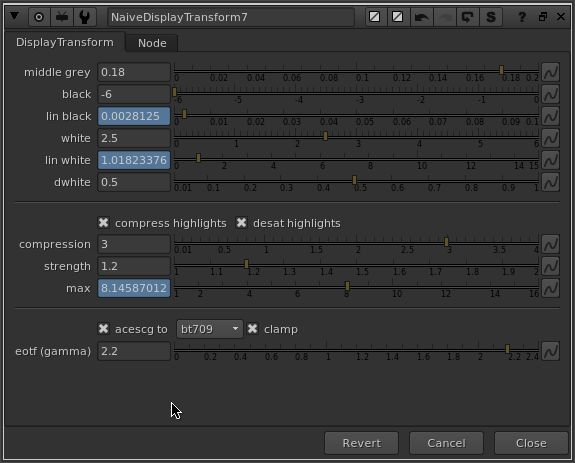
I reworked the parameters so that the naming is more consistent, and so that the linear value that is calculated is displayed right below the value you are adjusting.
Everything functions the same way except for the limit parameter, which I’ve changed the name of to compression and altered how it works. Now instead of mapping infinity to the value that you specify in stops above lin_white, you specify a value in stops above lin_white, and that value is compressed to display maximum. In other words, compression calculates the max value, which is the maximum scene-linear value that will be represented on the display.
I’ve also exposed the strength parameter, so you can adjust the slope of the compression curve. It seems like you need control over this to get the best results, depending on the dwhite and compression value you have set.
As before here’s a little video demo of the updates and changes I’ve made.
EDIT - Here is the nuke script described in the above screenshot
NaiveDisplayTransform_v02.nk (6.9 KB)
I also made some further usability improvements and additional parameters, which I did not make a post about. Here is that updated version:
NaiveDisplayTransform_v03.nk (7.6 KB)