As Nick pointed out, my DCTL were not that right. I’ve just corrected them, and also added global exposure compensation.
Thank you for sharing us.
I’m so glad you shared this information.
I read the pdf and your DCTL(below).
if(r <= 0.182){
r = r * 0.0625 * 1.8;
}else{
r = (_expf((r - 0.377675) / 0.182) / 30) * 1.8;
}
This 1.8 is EI from graph of Log1 curve?
Is this 1.8 necessary?
What does this mean by the added 1.8?
This sentence was written at the beginning Introduction of the PDF.
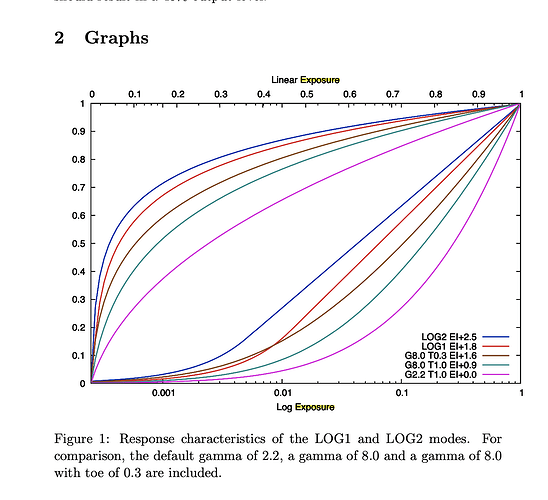
This documents presents the transfer curves that are obtained by setting various gamma, toe and log parameters. The curves are shown both against linear (bottom set of curves) and logarithmic exposure levels (top set of curves), on the same graphs. Black is 0.0 and white is 1.0 at both input and output.
For each setting, the exposure index correction in stops is shown. The exposure correction is based on the requirement that a 18% gray object should result in a 40% output level.
#Log1 Curve
a = 0.182
b = 30.0
c = 0.011375
d = 0.0
e = 0.377675
s = 16.0
grey = 0.18
log1 = a * math.log(b * grey + d) + e
print(log1)
> 0.6845996095497816
# Gamma Curve of Phantom
grey = 0.18
grey_18EI = 0.18 * math.pow(2.0, 1.8)
G = 2.2
T = 1.0
gamma = 1/(1 + 1.19 * (G - 1))
epsilon = 0.02 * T
PhantomGamma = (math.pow(grey + epsilon, gamma) - math.pow(epsilon, gamma))/(math.pow(1 + epsilon, gamma) - math.pow(epsilon, gamma))
print(PhantomGamma)
> 0.3904882254553703
PhantomGamma = (math.pow(grey_18EI + epsilon, gamma) - math.pow(epsilon, gamma))/(math.pow(1 + epsilon, gamma) - math.pow(epsilon, gamma))
print(PhantomGamma)
> 0.7866953781978775
Doesn’t this merely indicate that the Log1 Curve is as high as EI1.8 compared to the Default gamma2.2 T1.0 setting, which outputs 18% grey as 40%?
Upon checking, EI 0 with Gamma 2.2 and T1.0 resulted in approximately 40%.
The log1 value also seems to roughly match the graph.
However, even when adding EI 1.8 to Gamma 2.2 T1.0, it didn’t come close to the Log1 value.
Around 1.4 was closer.
Does anyone understand what this means?
Hello Kazuki, and thanks for your input. TBH, this discussion may already have gone a bit far for me, but I’m trying to catch up. If I look stupid at some point, well, it’s probably because I am…
The 1.8 and 2.5 factor I added are indeed the EI +1.8 and 2.5 we can see associated with LOG1 and LOG2.
Originally, I didn’t use those, but Nick Shaw suggested I should. Maybe I misunderstood what he was suggesting, or forked up on how to add them.
I just had some more tests this morning, with image rather than maths, and here is my view :
• Phantom raw set as LOG1, and LOG1 DCTL EI+0 used gives a coherent result.
• Phantom raw set as LOG2, and LOG2 DCTL EI+0 gives the EXACT same image as above.
• Both are less contrast and with higher gamma than the REC709 output. This is expected, as Phantom REC709 is what we wanna get rid of since it embeds some contrast manipulation, that are absolutely not documented.
So far, I have no idea how to understand those EI+1.8 and 2.5, but it seems quite clear we should NOT use them.
Here are DCTLs with no exposure compensation : Dropbox
And here is the test comparing REC709 against LOG1 and LOG2
Thank you for testing.
Is it correct that this video testing is below pipleline
・CineRaw Rec709 Debayer
・CineRaw Log1 Debayer > Log1 to Linear DCTL v3 > CST effect Rec709 Linear to Rec709 Rec709 gamma
・CineRaw Log2 Debayer > Log2 to Linear DCTL v3 > CST effect Rec709 Linear to Rec709 Rec 709 Gamma
I’d like to try it, but I don’t currently have any Cineraw files on hand to test with.
Does the pipeline below match Rec709 debayer?
・CineRaw Log1 Debayer > Log1 to Linear DCTL v3 > Linear to Gamma2.2 T1.0 DCTL (Lin_to_PhantomGamma22)
__DEVICE__ float PhantomGamma22_to_Lin(float PhantomGamma22){
float G = 2.2f;
float T = 1.0f;
float gamma = (1.0f)/(1.0f + 1.19f * (G - 1.0f));
float epsilon = 0.02 * T;
float lin;
lin = (_powf(PhantomGamma22 * (_powf(1.0f + epsilon, gamma) - _powf(epsilon, gamma)) + _powf(epsilon, gamma), (1/gamma))) - epsilon;
return lin;
}
__DEVICE__ float Lin_to_PhantomGamma22(float lin){
float G = 2.2f;
float T = 1.0f;
float gamma = (1.0f)/(1.0f + 1.19f * (G - 1.0f));
float epsilon = 0.02 * T;
float PhantomGamma22;
PhantomGamma22 = (_powf(lin + epsilon, gamma) - _powf(epsilon, gamma))/(_powf(1+epsilon, gamma) - _powf(epsilon, gamma));
return PhantomGamma22;
}
Yes, that’s correct.
That can be easily fixed. I have hundreds TB of them.
Unfortunately, I don’t know how to split those files to shorter segments…
I’ve found one clip though that is very short, and weights less than 1GB :
For some reason, I can’t figure how to make your dctl works properly.
I hope you can answer your own question with provided footage…
I checked the Cineraw Rec709 Debayer(Resolve) and Gamma2.2 T1.0 DCTL
It did not match.
Cine Raw Rec709 Debayer
Gamma2.2 T1.0
( CineRaw > Log1 Debayer > Rec709 Log1 to Rec709 Linear > Rec709 LInear to Rec709 Phantom Gamma2.2 T1.0)
You’re trying to compare LOG version with REC709, but it is taken from granted that their REC709 has some contrast added, as I mentioned before. So from my own understanding, it does not match and that’s good news! Gamma 2.2 T1 is in fact the real REC709, with no added manipulation…
I am only guessing in terms of what is intended by the EI offsets. But if you just apply the formulae as is, then a log value of 1.0 maps to a linear value of 1.0, which is where ACES expects diffuse white to be. You have no highlight detail.
Applying a gain of 2^1.8 or 2^2.5 (not just 1.8 and 2.5, assuming the values are in stops) will create values >1.0, putting some pixels into the highlight/specular region. Of course this will only work if the footage has been exposed with this in mind. I do not know what exposure tools are available on the Phantom, and therefore where you might end up placing mid grey in the log signal.
I have no Phantom footage to test with.
The exposure correction is based on the requirement that a 18% gray object should result in a 40% output level.
I am confused by that, as it does not seem to be the case, whatever you interpret the EI offsets to mean.
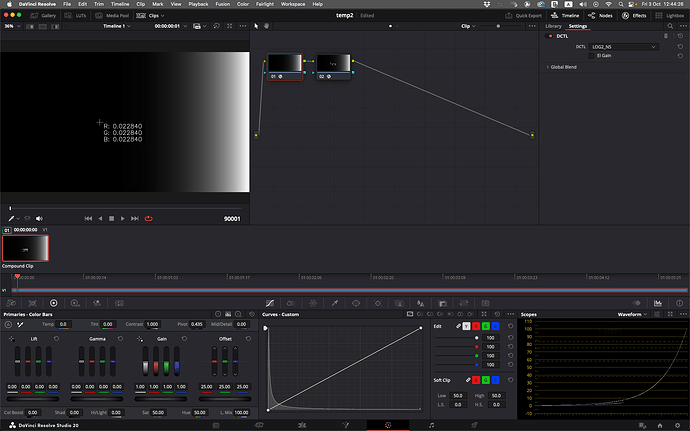
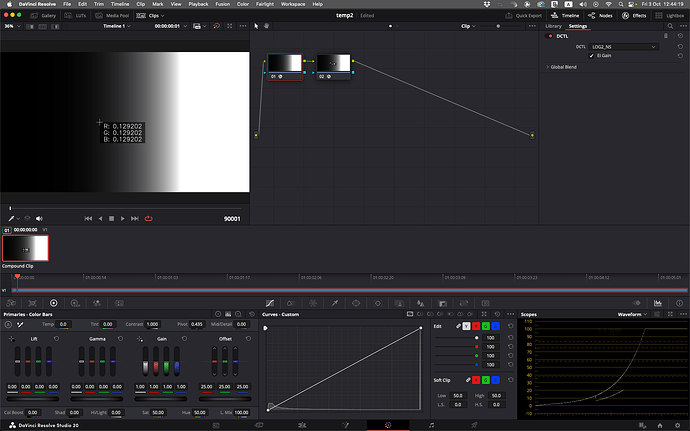
taking the formula as written, a Log2 vale of 0.4 maps to a linear value of 0.02283986. Multiplying this by 2^2.5 gives 0.12920176. Neither of these are 0.18, the expected linear value of mid grey.
Using the DCTLs below, and sampling 40% of the way across a linear ramp, verifies my result above.
LOG1_NS.dctl (786 Bytes)
LOG2_NS.dctl (786 Bytes)
I also checked this EI using a Log1 curve, but I couldn’t figure it out.
Only at Gamma 2.2 and T1.0 did the values appear to satisfy EI0.
The conditional expression may be incorrect.
//David v3
//if(r <= 0.182){
// r = r * 0.0625;
//}else{
// r = (_expf((r - 0.377675) / 0.182) / 30);
//}
//
if(r <= 0.182 * 16.0f){
r = r * 0.0625;
}else{
r = (_expf((r - 0.377675) / 0.182) / 30);
}
This is a different question,
but I tried implementing it in CLF and the results didn’t match.
What do you think is different?
<Log inBitDepth="32f" outBitDepth="32f" style="cameraLogToLin">
<Description>Phantom Log1 to Linear</Description>
<LogParams base="2.718281828459045"
logSideSlope="0.182" logSideOffset="0.377675"
linSideSlope="30.0" linSideOffset="0.0"
linSideBreak="0.011375"
linearSlope="16.0"/>
</Log>
The values obtained when using this CLF with OCIO tools differed from the values obtained when using Resolve 20.2.3.
According to Blackmagic,
it was a bug where the CLF Log tag did not support floating point values.
They plan to address this in a future update.