About Chroma Compression
Chroma compression seems to be a common source of confusion so I will take a try at explaining it better. I did attempt to explain why it is a necessary component of a display transform at the beginning of this thread quite a while ago, but I’ve learned a lot since then so maybe it’s time for another stab at it.
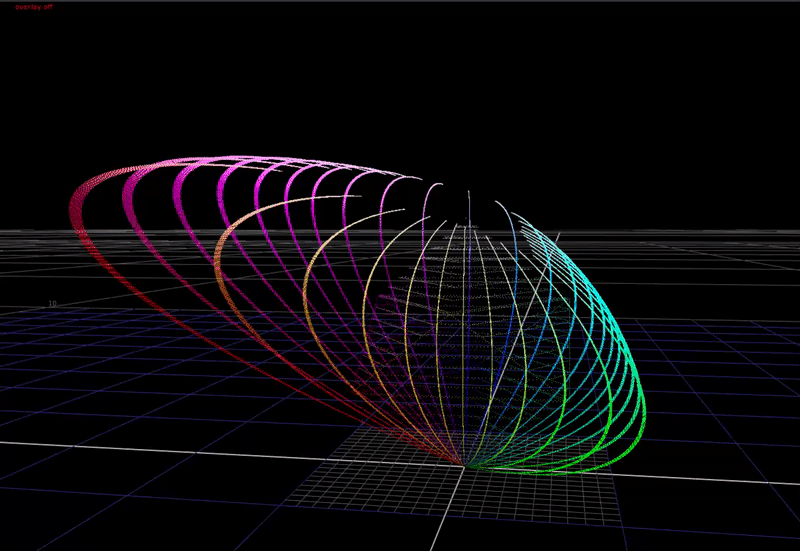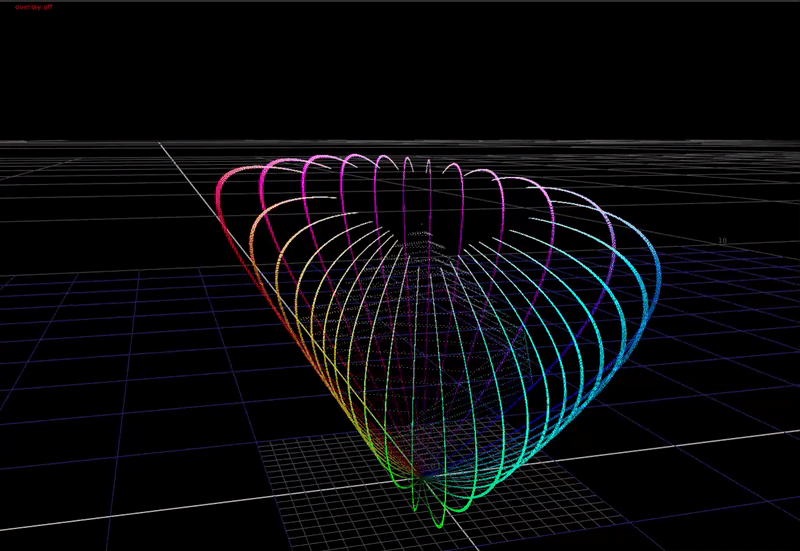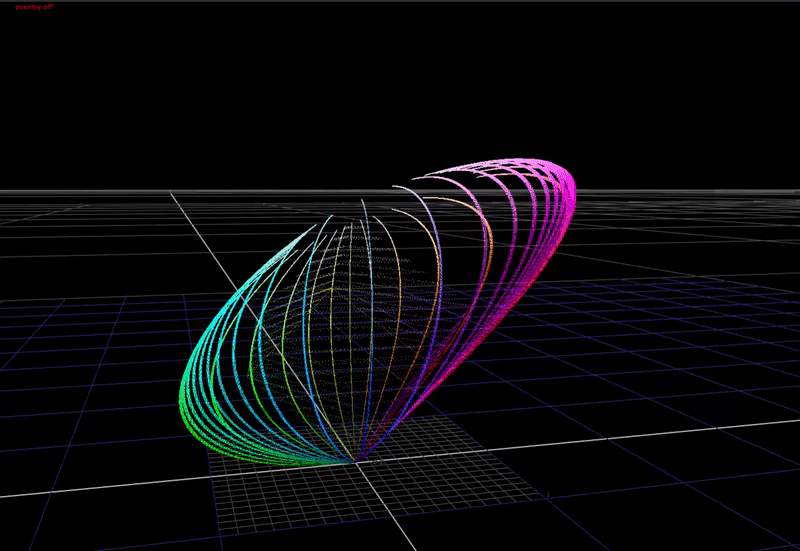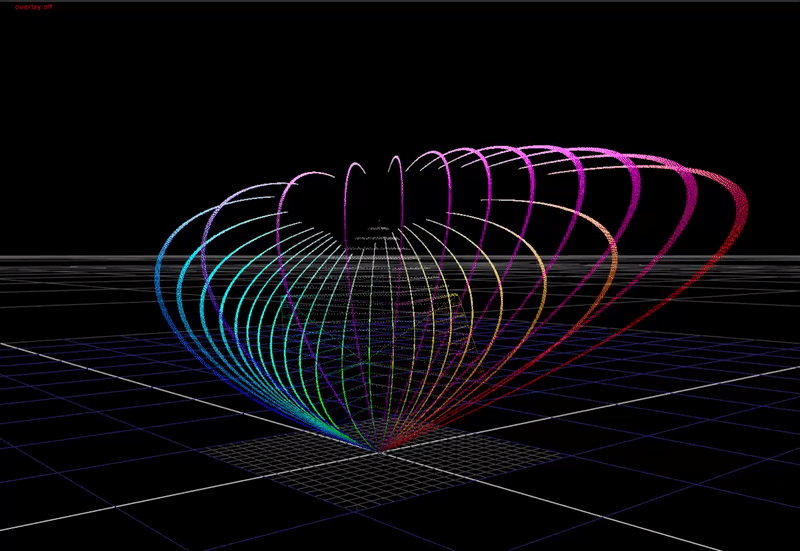
First a definition of the problem. In a display transform we must remap scene-linear to display-linear. What does this mean? In scene-linear we are dealing with a large range of values without an upper bound. Here’s a plot of a hue sweep, animated from 0 chroma to 100% chroma, plotted in RGB. The input intensity ranges from 0 to 6 stops above 18% grey.
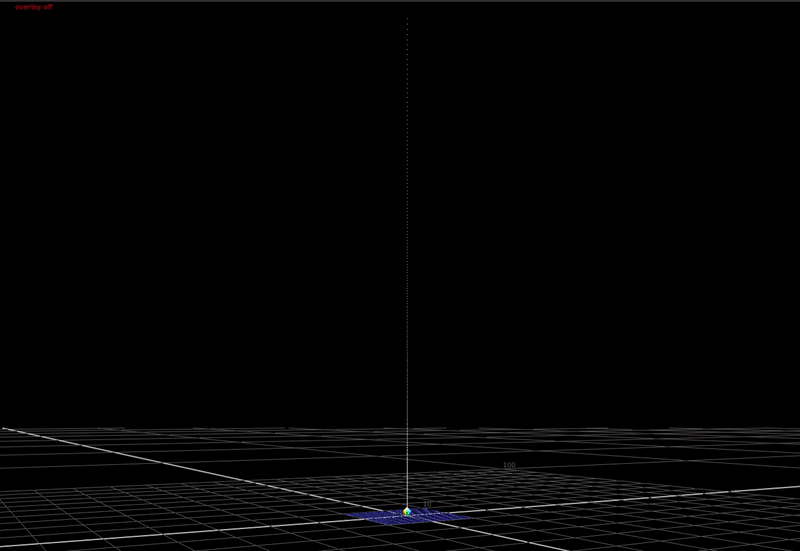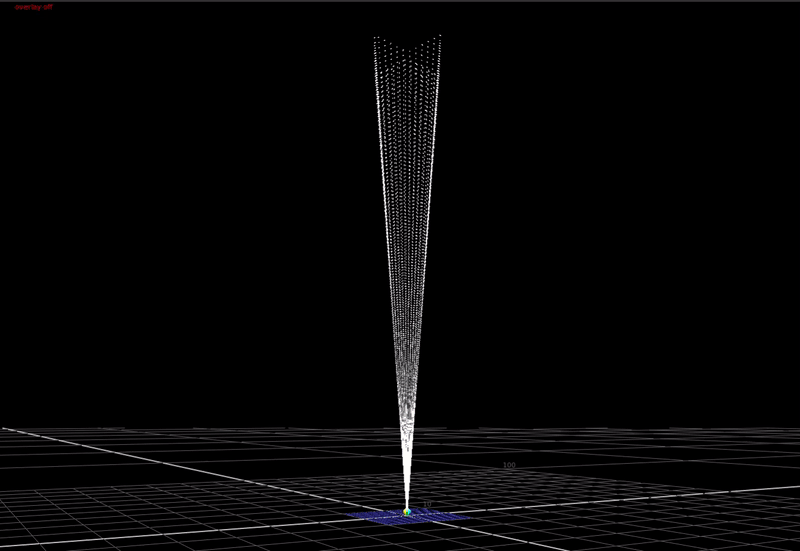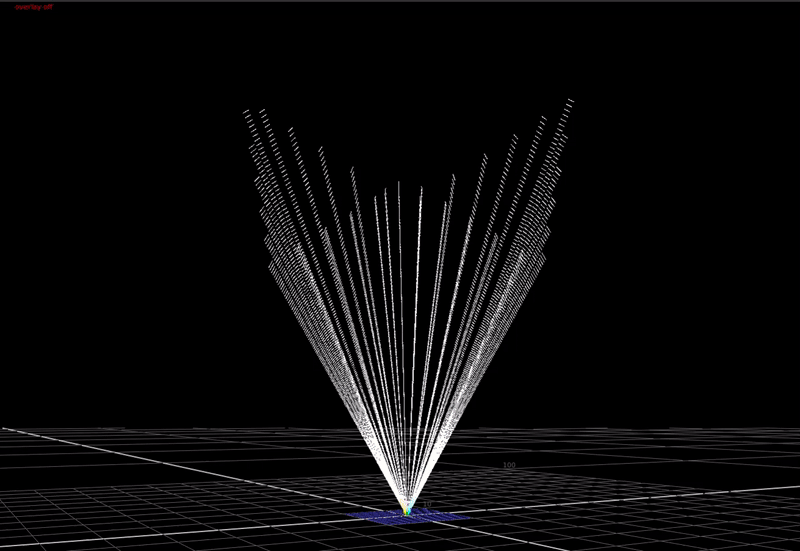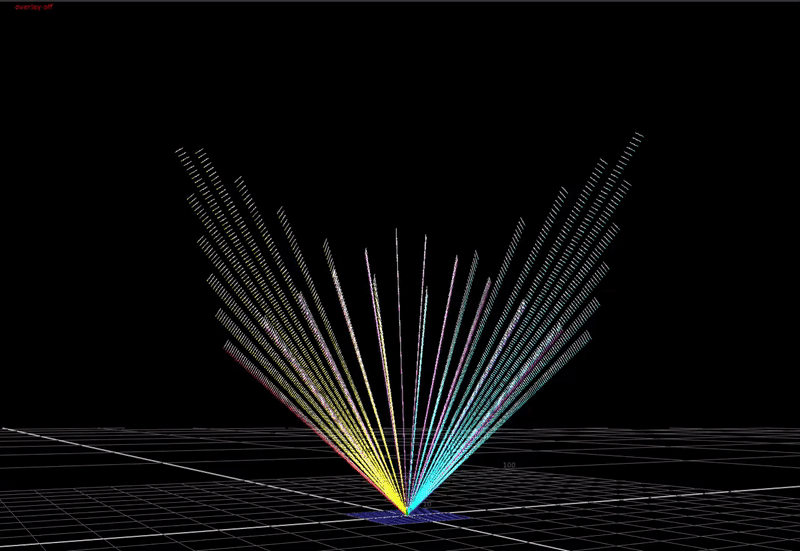
In a display transform we need to map this large range of input values down into a little cube: the bounded display-referred gamut volume.
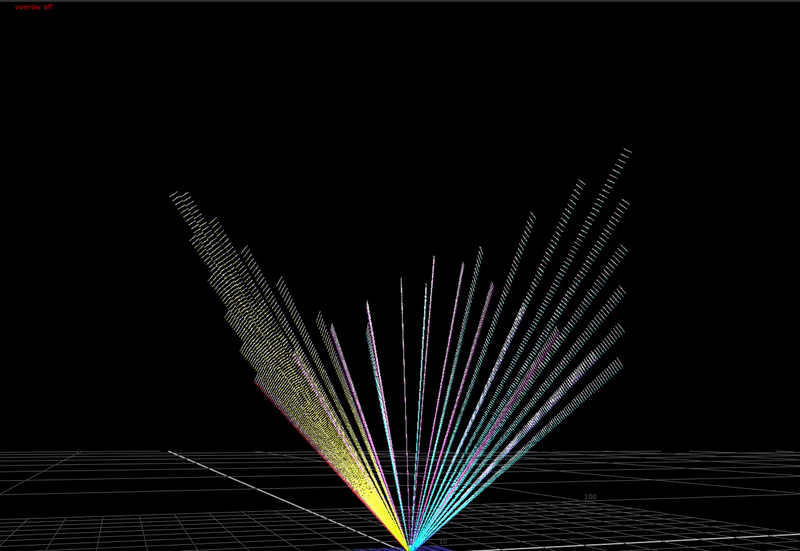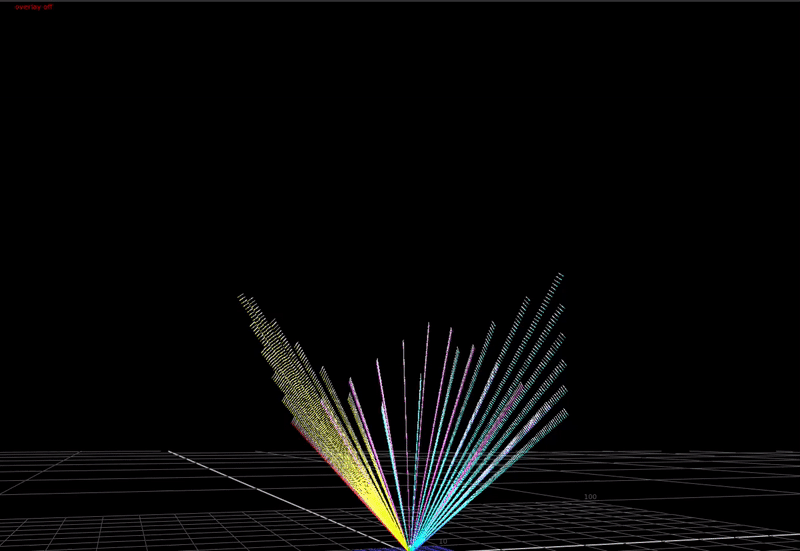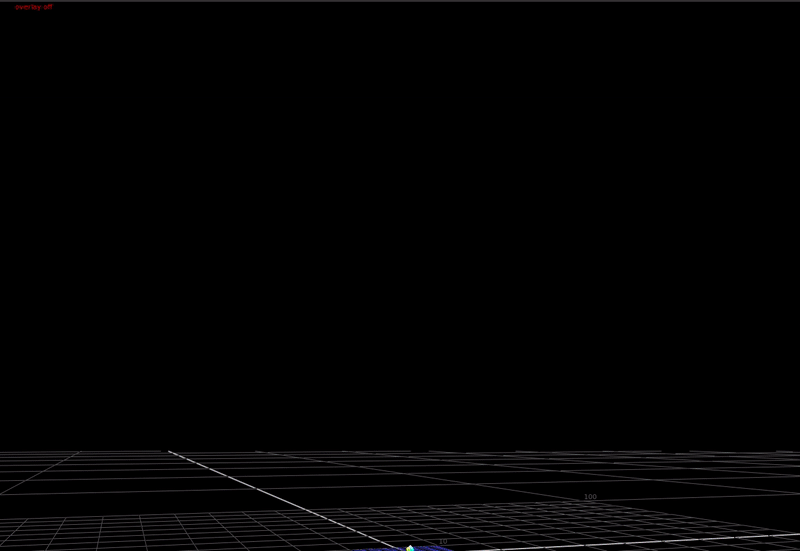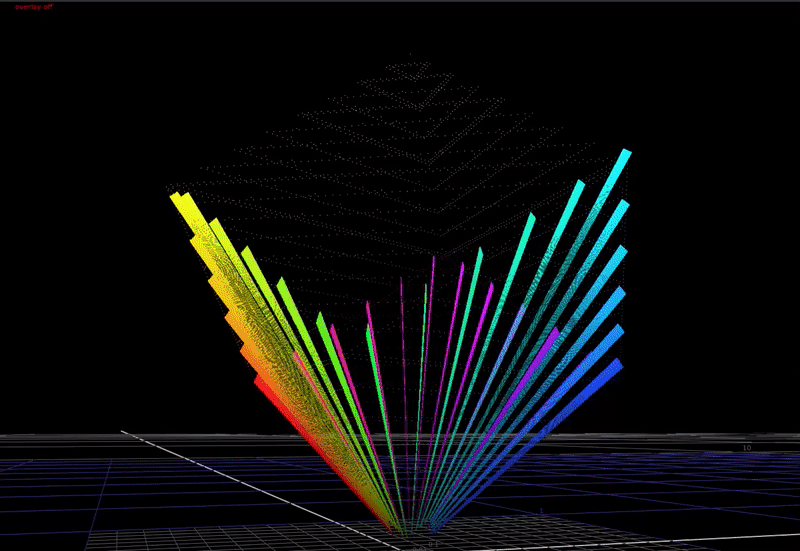
In the 3-dimensional RGB space, the plot of all saturated colors forms an inverted pyramid.
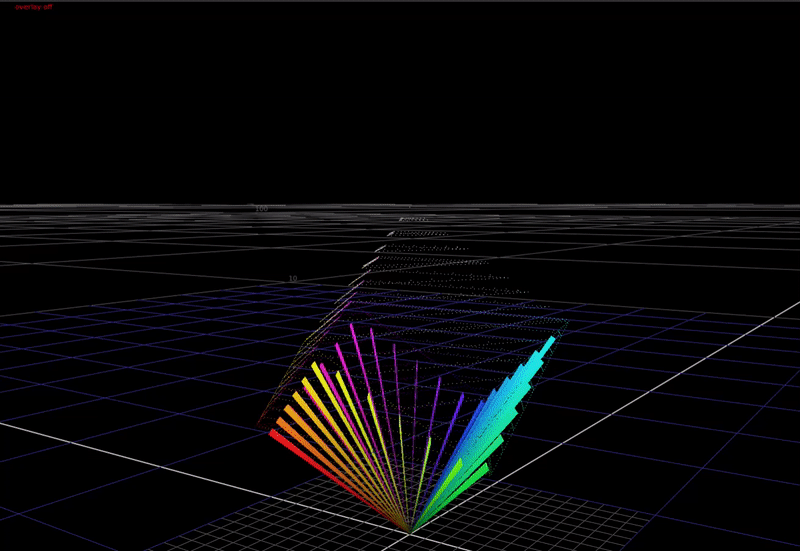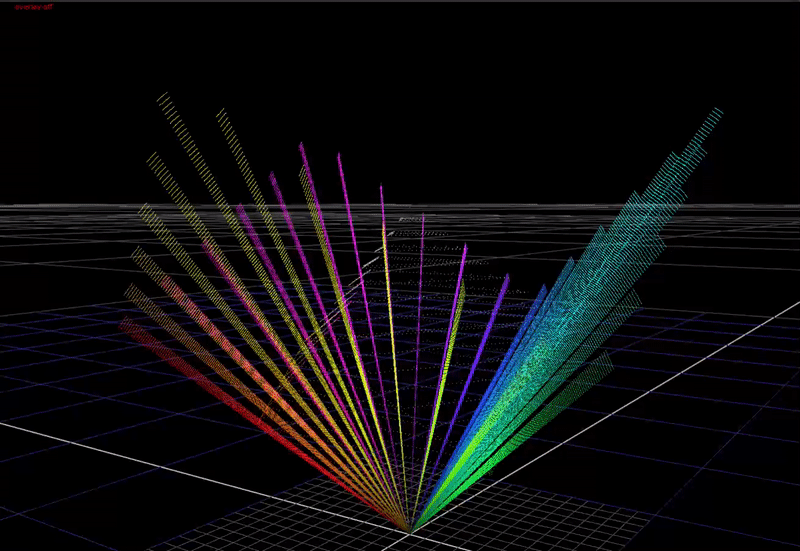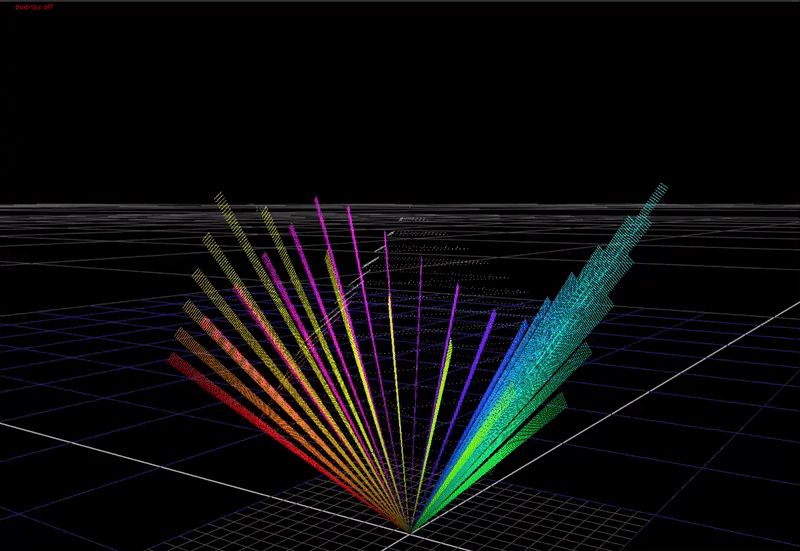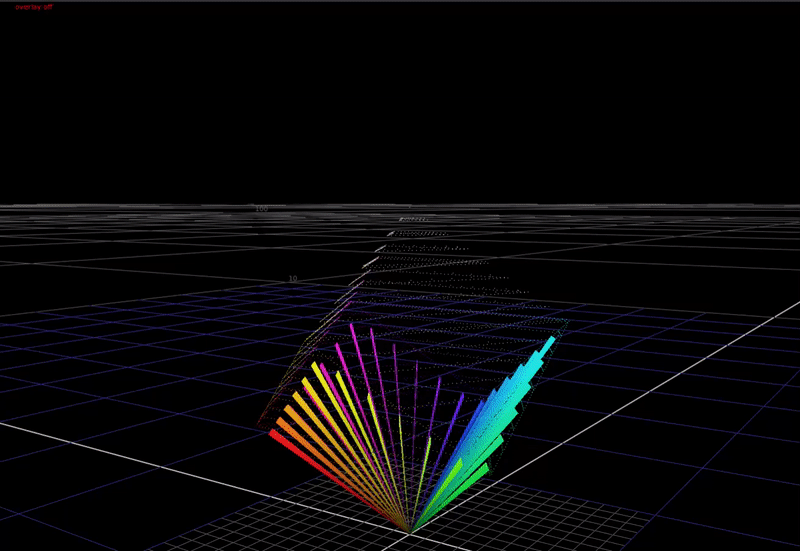
As you can see above, if we just compress saturated colors into the display gamut cube without changing the colors, we aren’t using the top half of the cube! That’s a lot of wasted area we could use for making nice looking images.
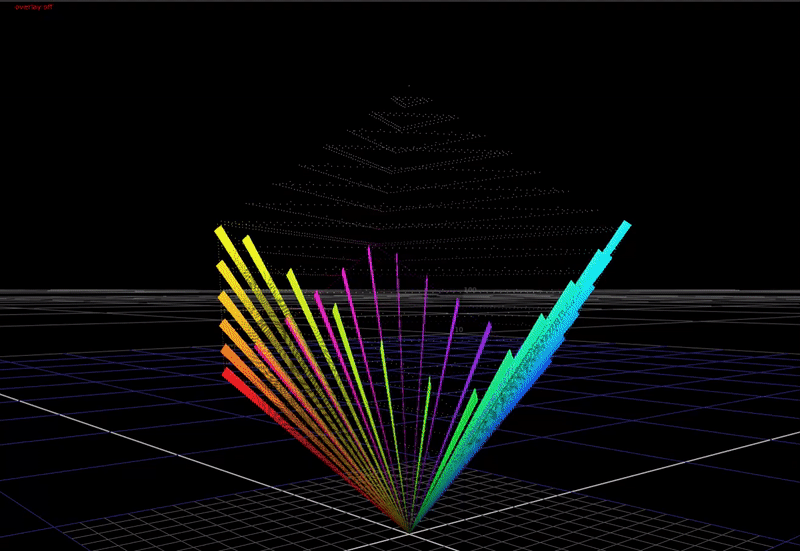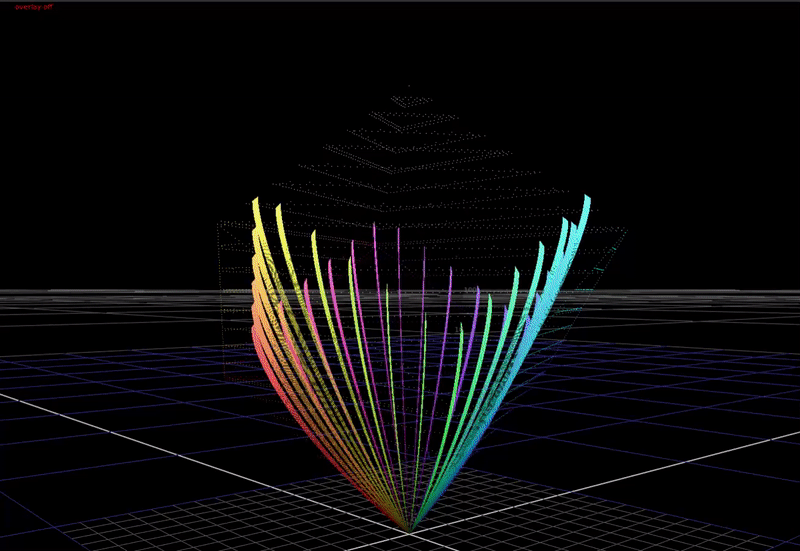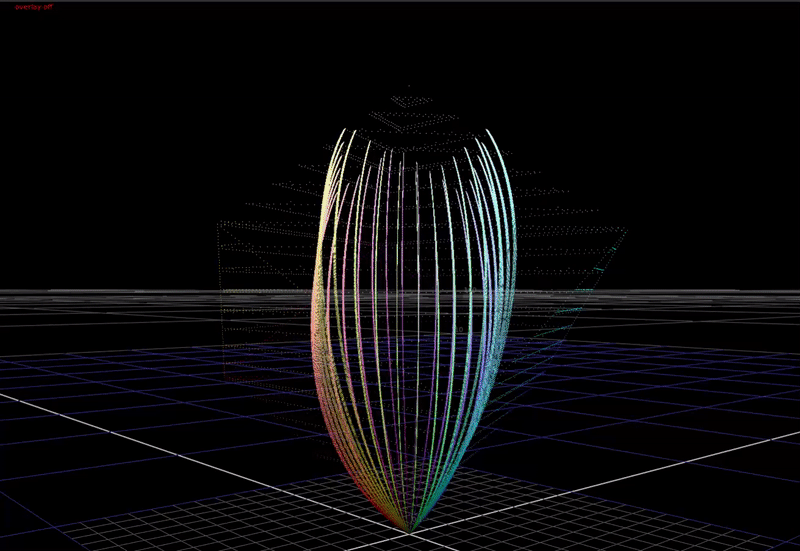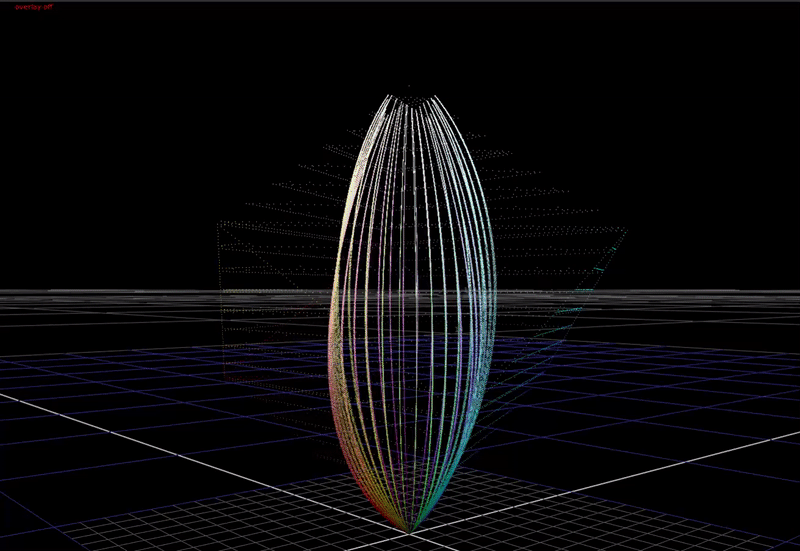
If we compress the chroma of saturated colors towards the achromatic axis with increasing brightness, this allows saturated colors to be rendered with more apparent brightness in the image. This is a cheat necessary because of the limited dynamic range of our display devices compared to the real world. In HDR, we have a higher available dynamic range in our display devices, therefore we need less chroma compression in the rendering for these devices.
Per-Channel Chroma Compression
First let’s take a look at what is happening in our familiar per-channel rendering approach.
Viewed from the side, with 80% chroma:
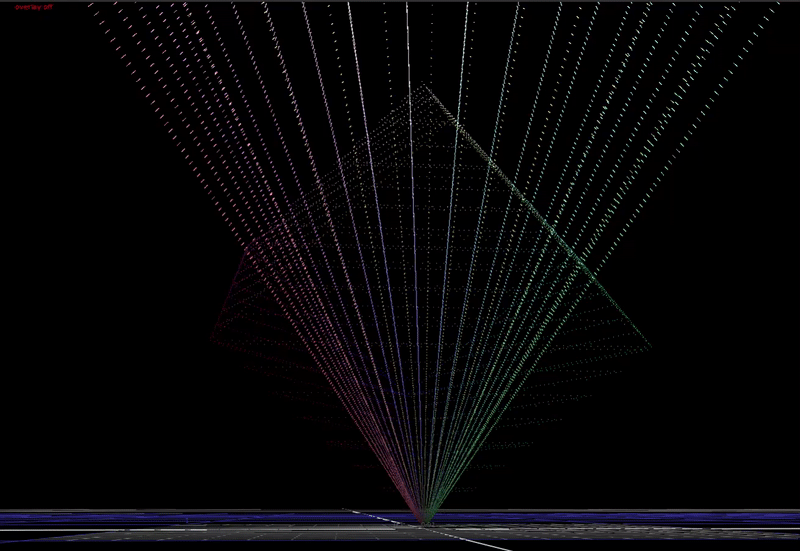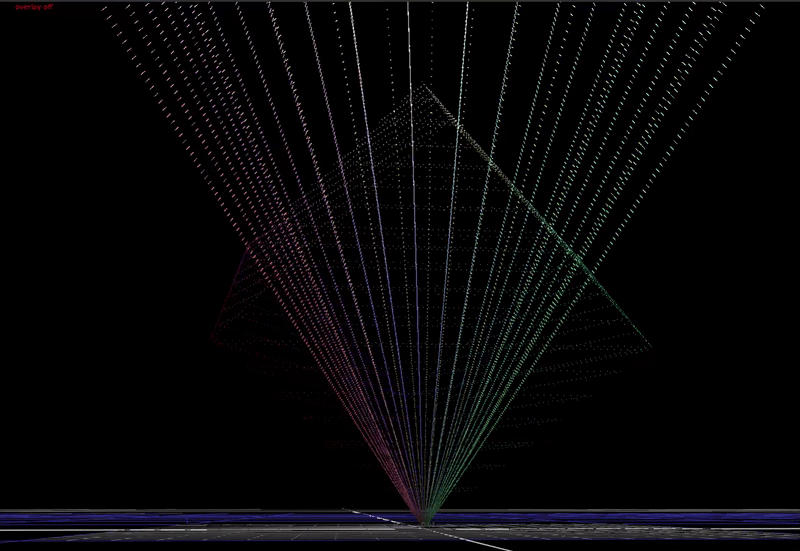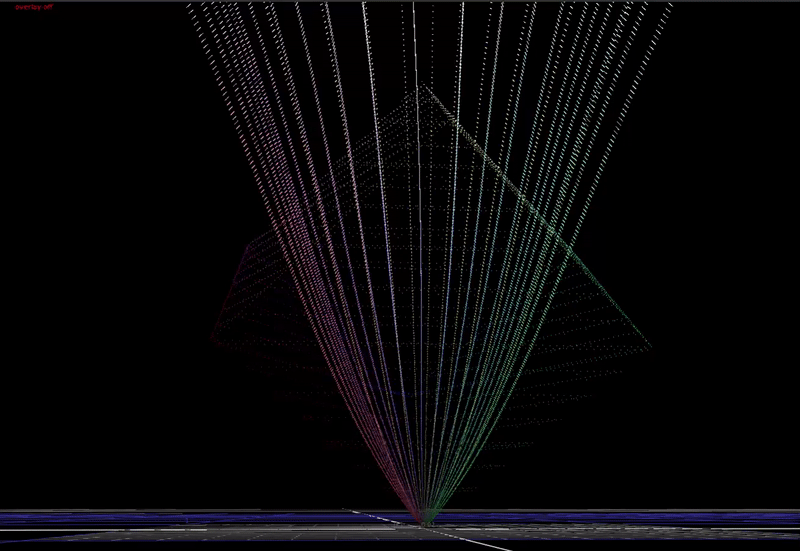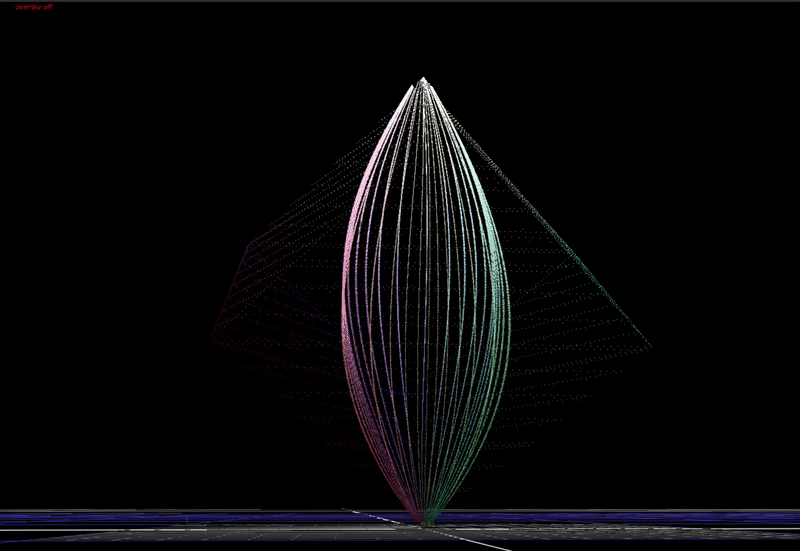
Note how chroma is being compressed above middle grey, and expanded below middle grey.
And with 100% chroma:

With more saturated input colors that near the edge of the display gamut cube, we can see much more significant distortions in hue as chroma is compressed. It’s also interesting that there are no values outside of the cube after compression.
Here is a view from the top, this time animating input chroma from around 50 to 100%.
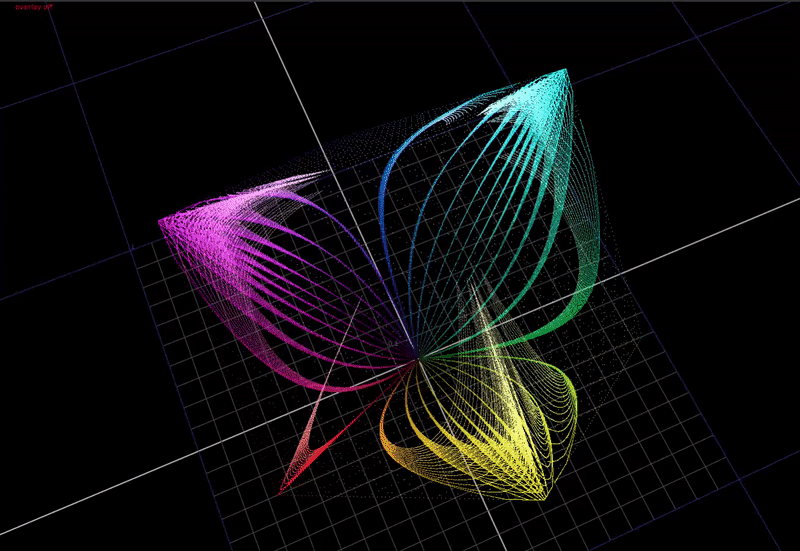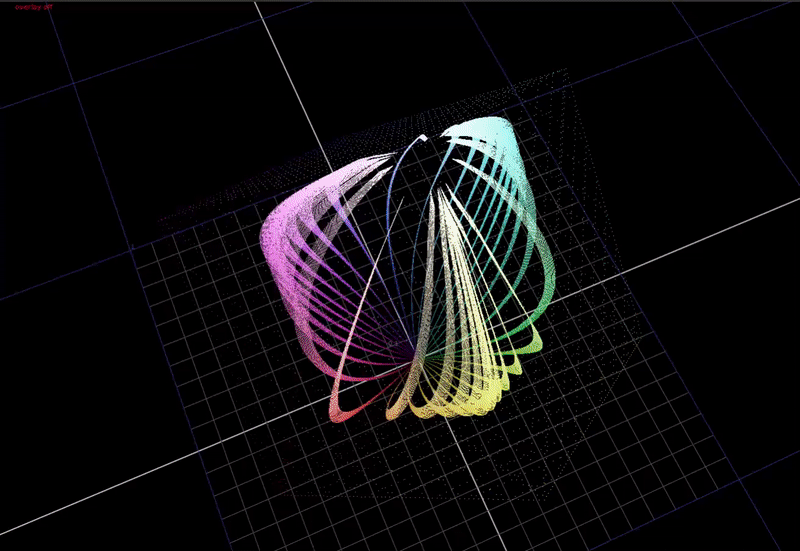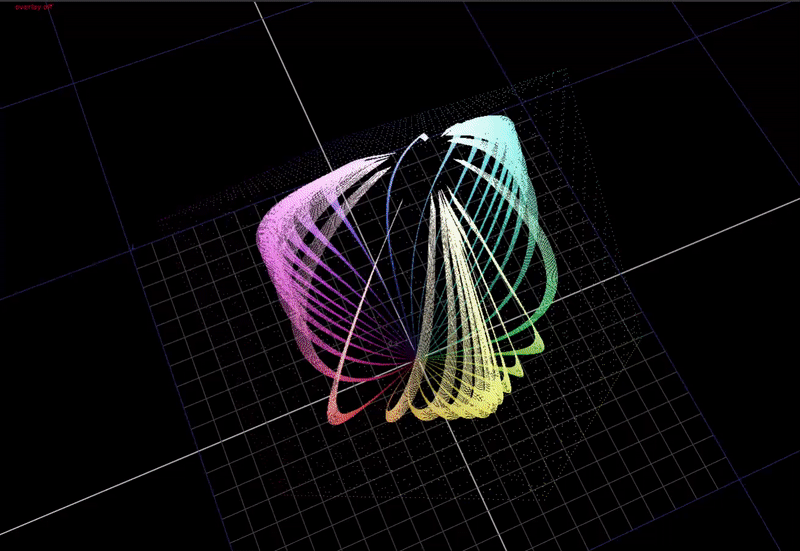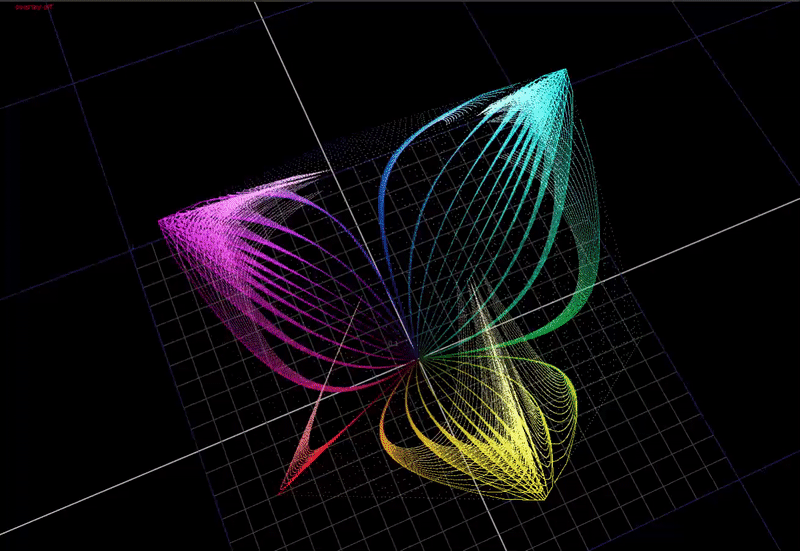
Note how how the hue distortions converge towards the secondary colors: cyan magenta and yellow. Red stays perfectly aligned.
But what if we do a very small 1 degree hue rotation on the input?
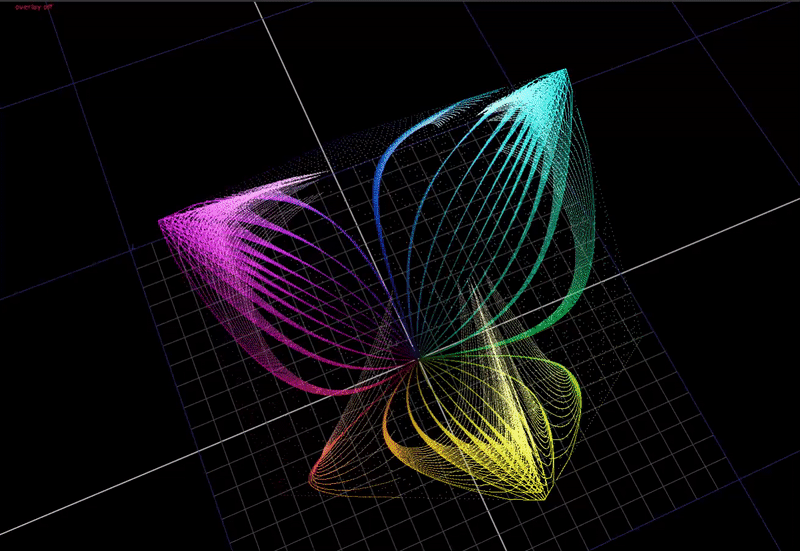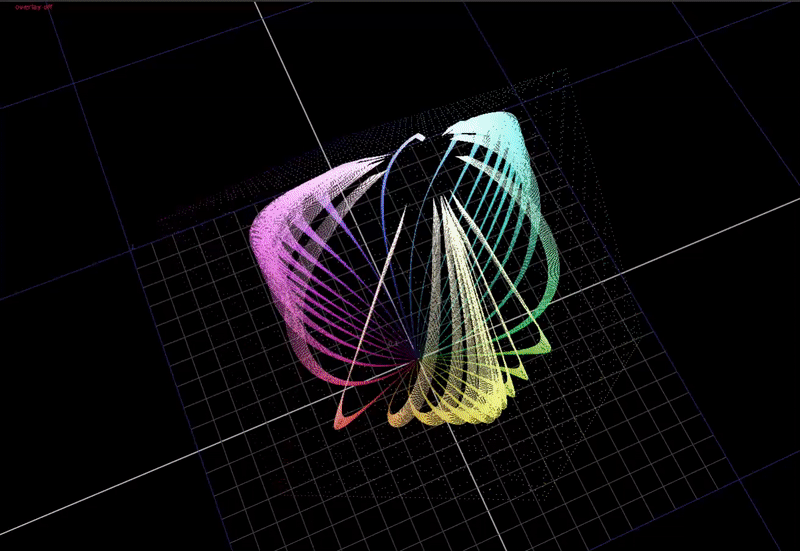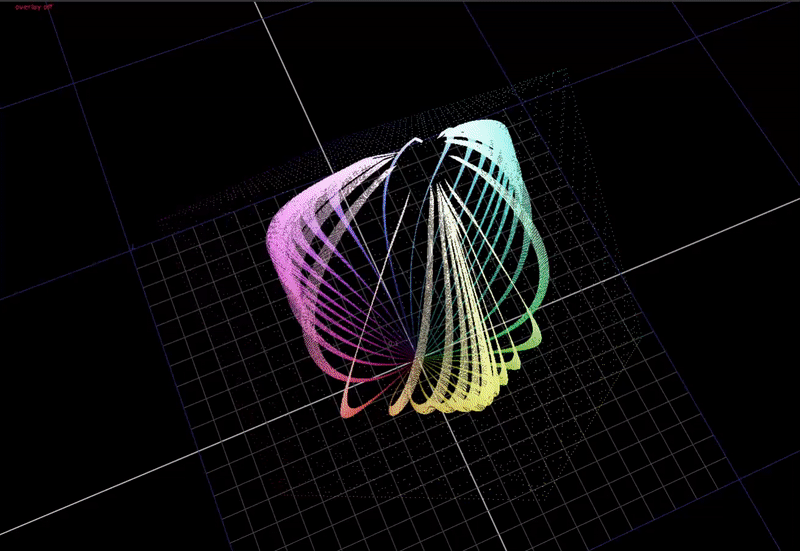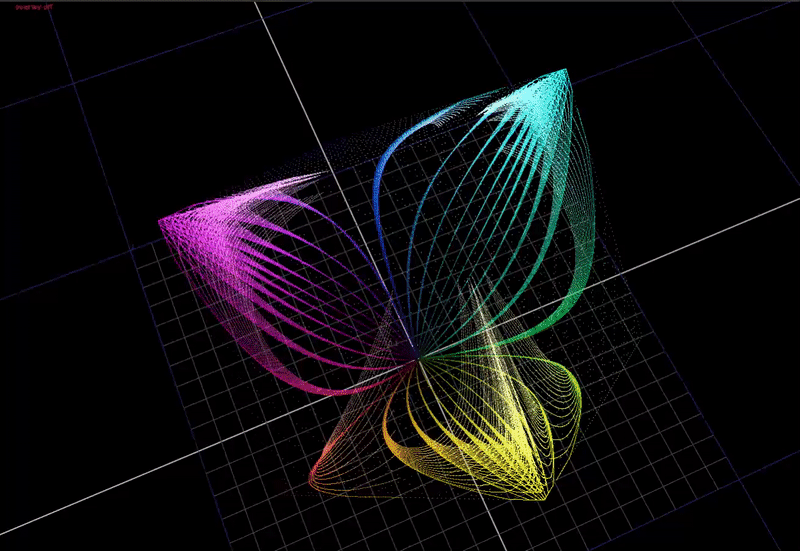
Now the hue that is very close to red is distorting significantly towards yellow at the top end.
OpenDRT Chroma Compression
Here is what OpenDRT’s chroma compression looks like:
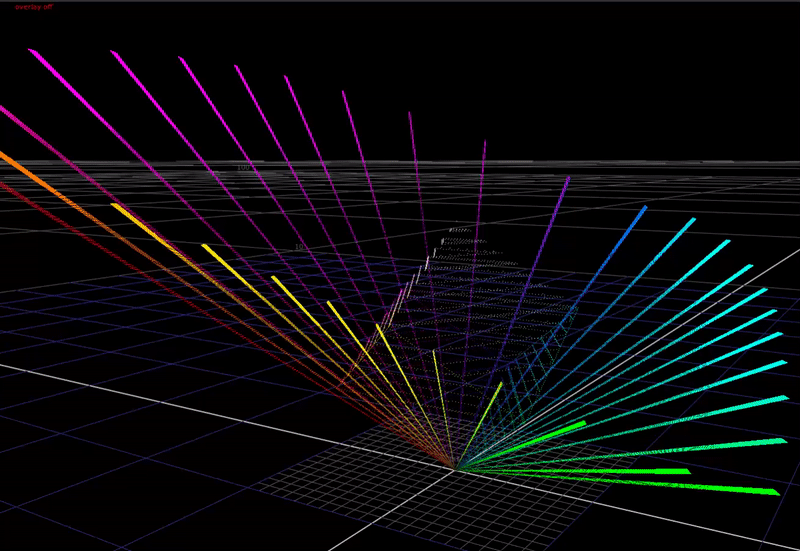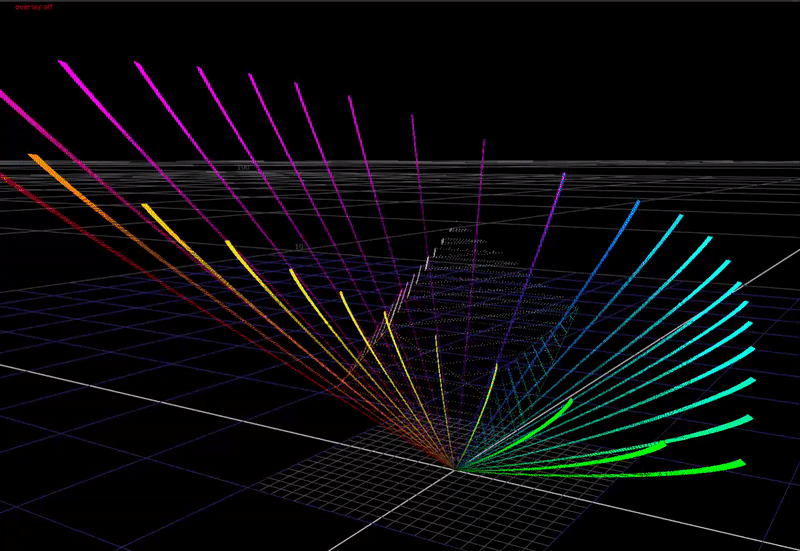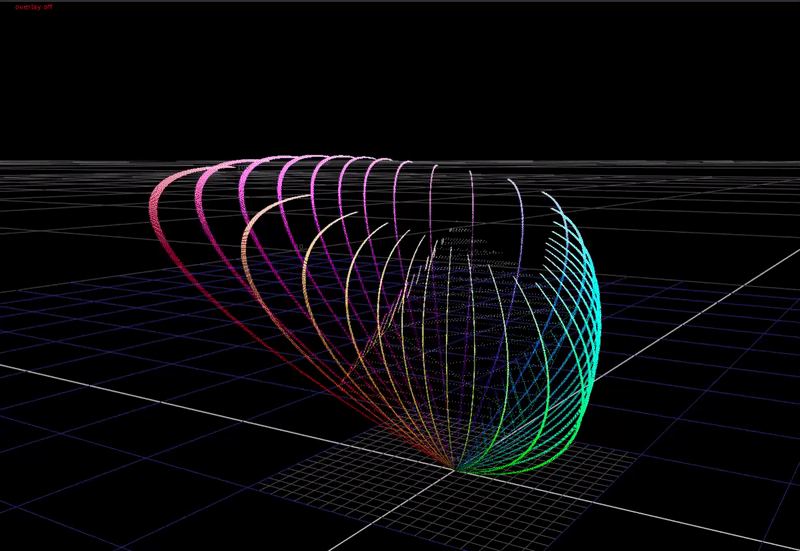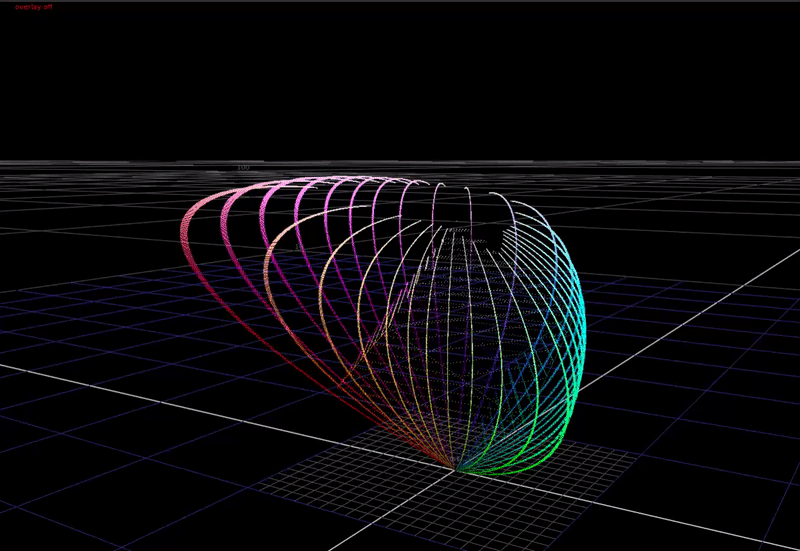
The algorithm is very simple, but there are a few key things that make it work well.
First, the math of the dechroma is a lerp towards an achromatic axis defined by some vector norm, controlled by some factor.
The norm is important because it controls the shape that the dechroma takes when compressed. OpenDRT uses a euclidean distance norm, with a weighting applied to the 3 channels. This norm forms a shape that compresses secondary hues more than primary hues, and works in our favor for pleasing image appearance.
The factor is derived from the highlight compression, and uses a simple hyperbolic compression function.
In simple psuedocode:
float3 rgb = <input vec3>;
float norm = sqrt(pow(rgb.x * 0.24) + pow(rgb.y * 0.1) + pow(rgb.z * 0.09));
float sx = 0.7; // input domain scale
float dch = 0.5; // dechroma strength (high end)
float sat = 1.2; // saturation strength (low end)
// chroma compression factor
ccf = pow(sx / (norm + sx), dch) * sat;
// apply dechroma with a lerp
rgb = norm * (1.0 - ccf) + rgb * ccf;
return rgb;
Another key aspect of the chroma compression is the domain that the compression is applied in. OpenDRT uses ~CIE 2006 LMS.
If we adjust the dch parameter, it affects the strength of the chroma compression at the “top end”.
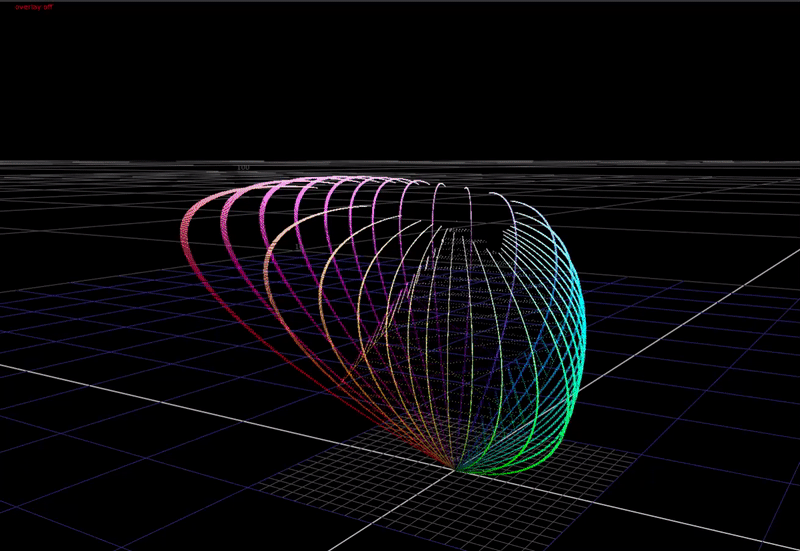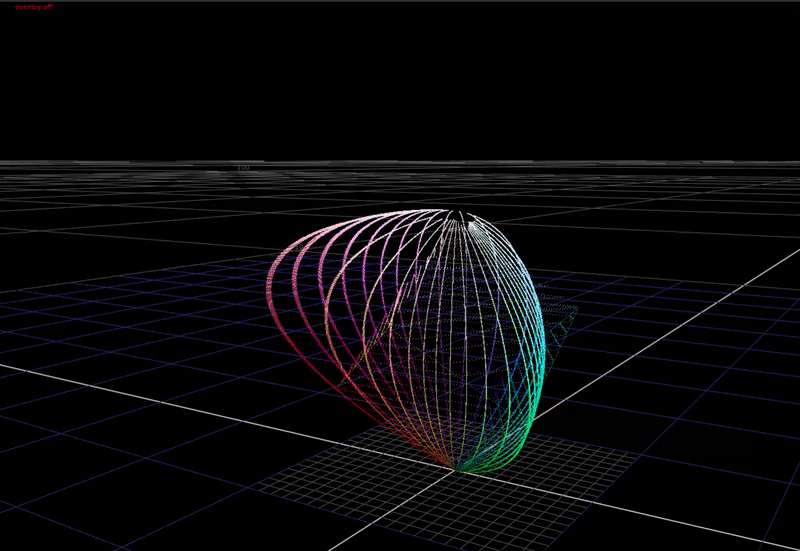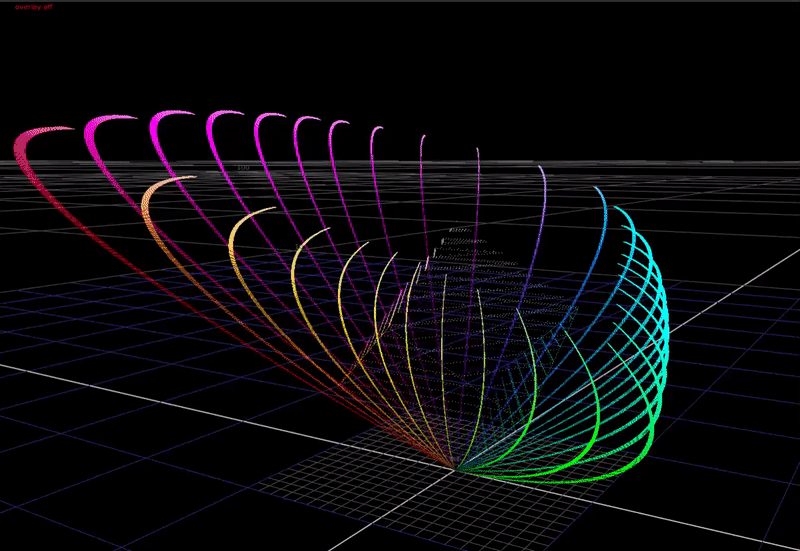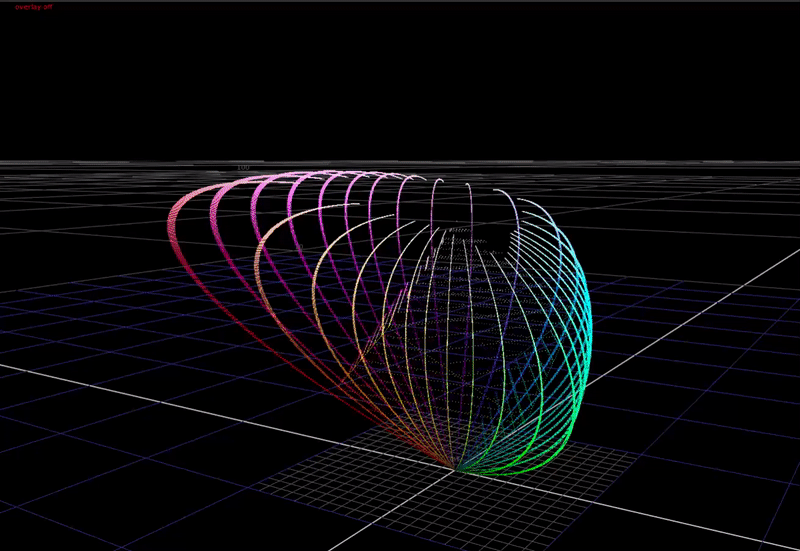
And if we adjust the sat parameter it affects more the chroma at the “bottom end”.
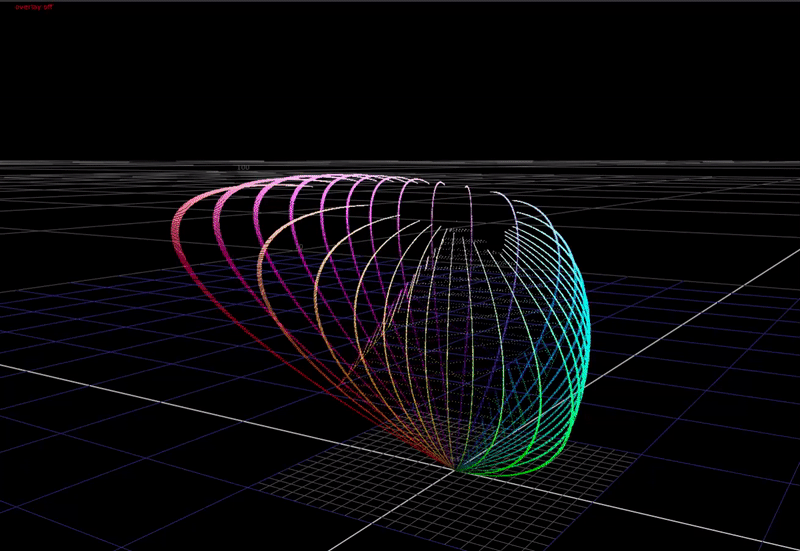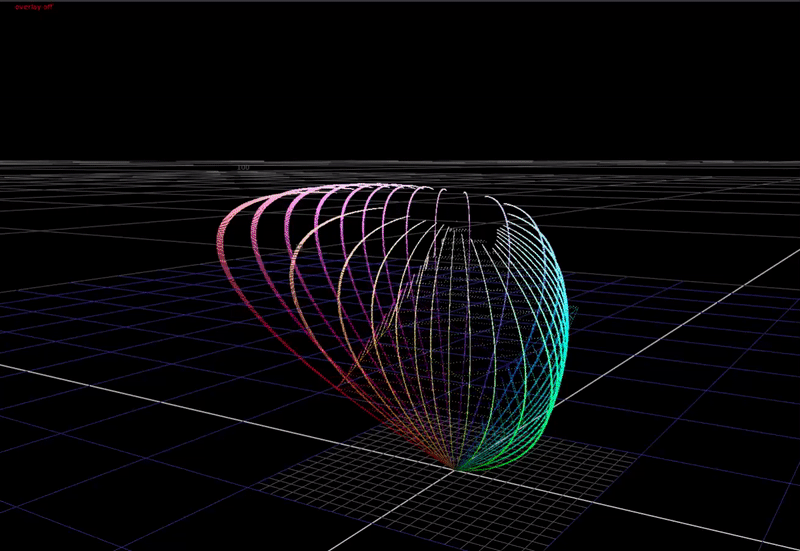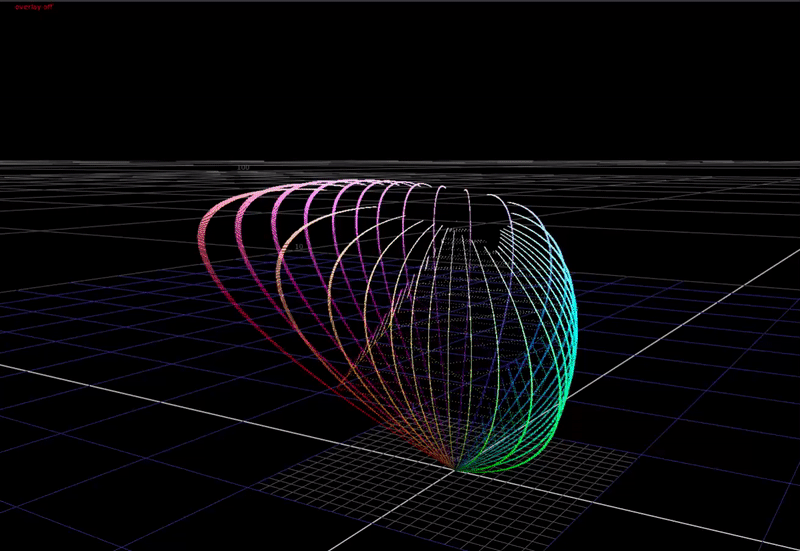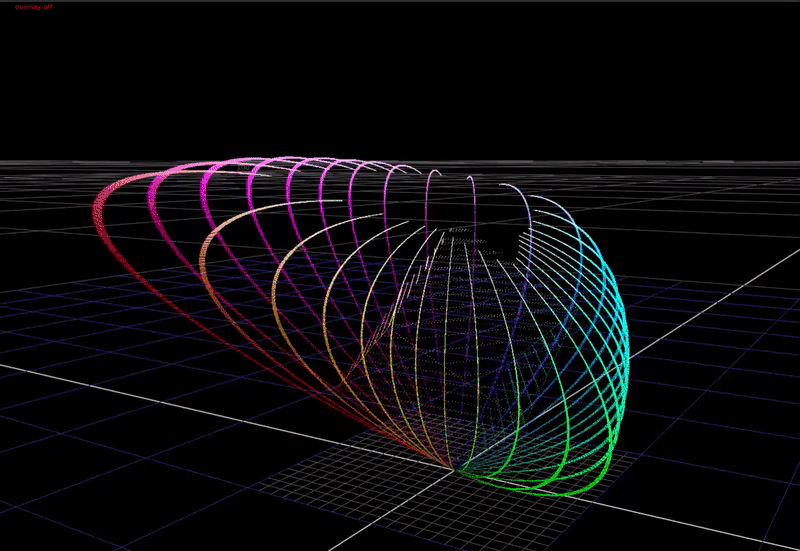
Represented above we have two different approaches. Per-channel is a “water fills cube” approach.
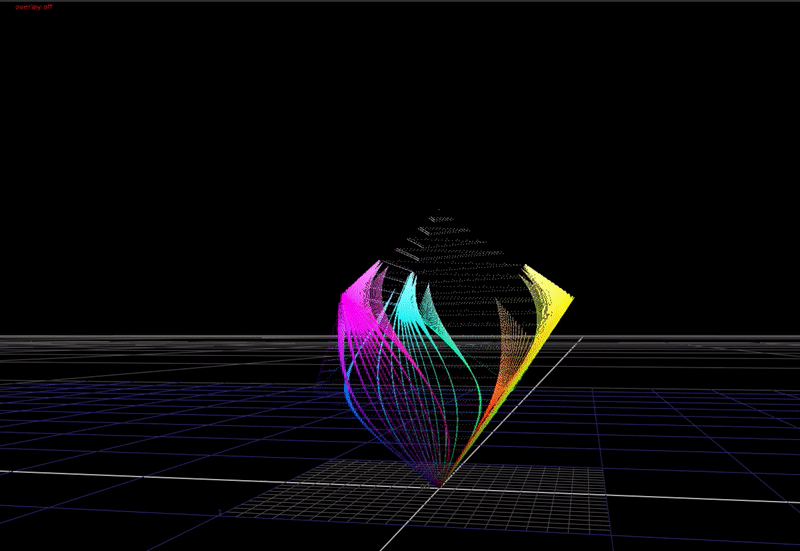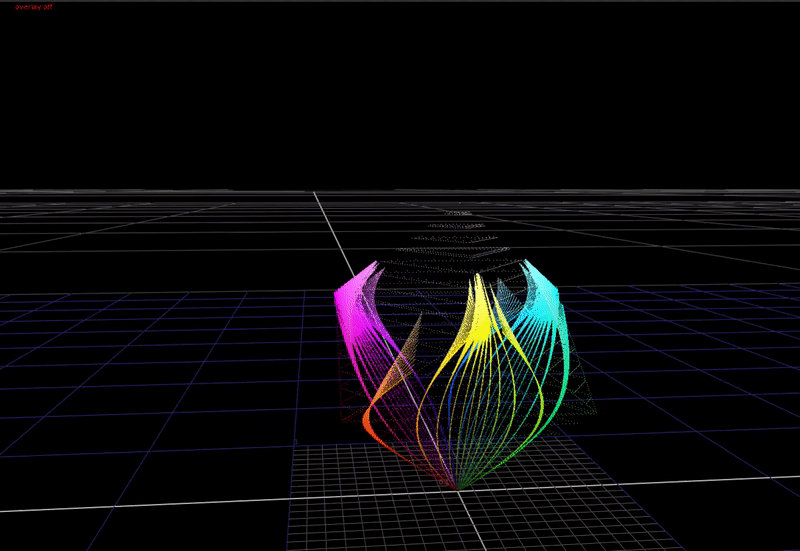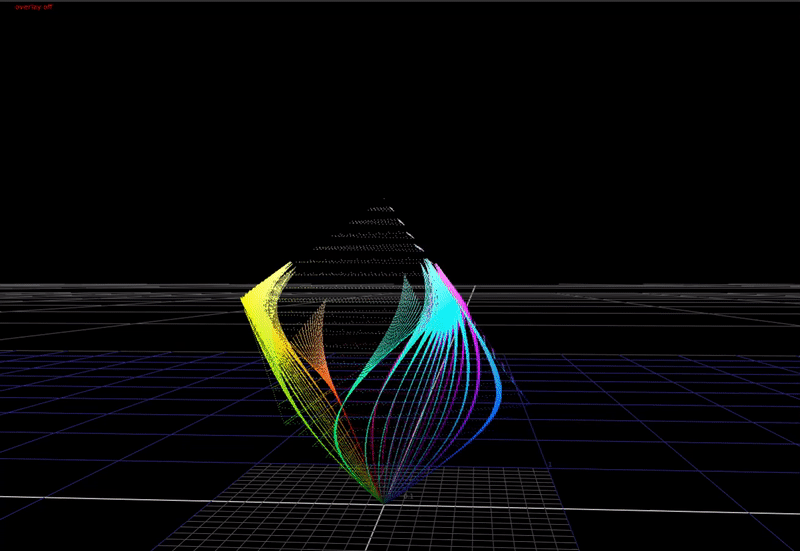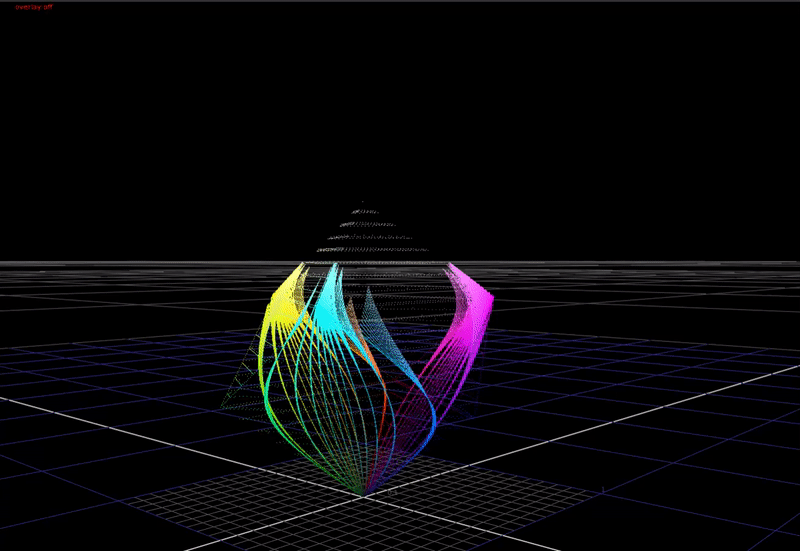
OpenDRT uses a “cube inside a balloon” approach.
As usual here is the nuke script I used to generate the above images if you want to play.
chroma-compression.nk (37.1 KB)