I don’t think I’ve sufficiently explained the problem that the shadow rolloff parameter on the gamut compress operator is trying to solve. I’ll try to elucidate that clearly here.
Distance in Shadow Grain
As we know the distance is our measure of the color purity, saturation, or distance from the achromatic axis. In our calculation of this distance we divide the inverse rgb ratios by the achromatic value in order to normalize the distance such that a distance of 1.0 is at the gamut boundary.
Because achromatic is in the denominator of this division, when achromatic approaches 0, distance approaches infinity. Because of this, it is common to get unnaturally large distance values in shadow grain.
In our example imagery, the largest distances of visible out of gamut colors aren’t that big - maybe a common maximum that is less than 2.0. See this big ramble for some examples. (I need to buff up my data analysis and plotting skills but you get the idea).
In shadow grain, you commonly see distance values of 4, 15, 48, 5000. Very large and very meaningless numbers.
The Problem
So what’s the problem? Our compression function compresses from the specified max distance to the gamut boundary. Large distances will be compressed some but they will still be kept large. For example with the current default values in our gamut compress operator, a distance of 48 in R would be compressed to 1.26732.
The problem comes about when we invert. In a vfx pipeline, most likely inversion would occur with 16 bit half float precision. A half float exr would be written out with gamut compression applied, and gamut compression would be inverted on an iteration of the same image. When our distance value of 1.26732 changes slightly, the inverted distance value changes dramatically. Say our distance is quantized to 1.26758 in half float. When inverted our new distance value is 55.78 instead of 48. This is a big difference!
The more aggressive the power function the worse the situation gets.
Give me Pictures
Enough verbosity, let’s look at some pictures.
I’ll use the “Party Off” clip (A003R3VC/A003C001_120101_R3VC.mxf) from @joseph as an example.
Here is the first frame.
Here is the inverse rgb ratios.
Here is the normalized inverse rgb ratios. Note how much brighter the shadow grain got.
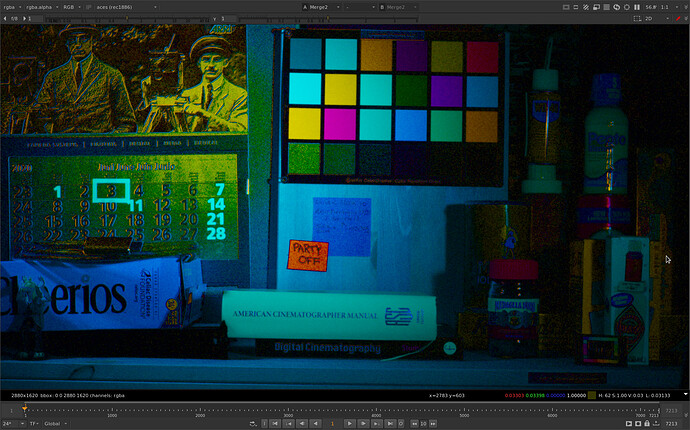
Here’s a detail view, gaining down and zooming in on the shadow grain. I’m sampling a pixel here that has a distance in G of 161.
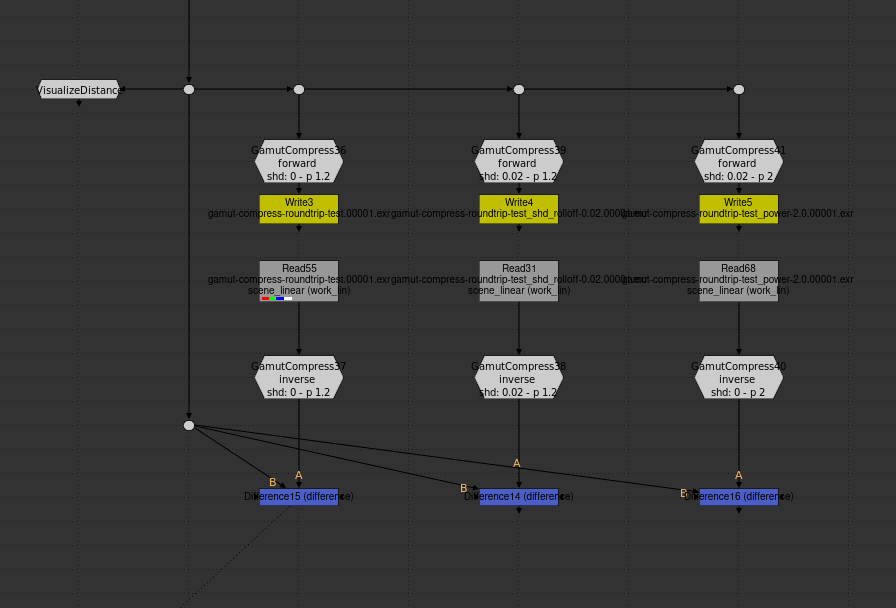
Now we can test inversion errors. I’m using a Nuke setup like this:
Basically, gamut compress with a particular setting, write the result out as a 16 bit half float exr, read it back in, invert the gamut compression, and compare to the original.
Looks good to me! Except… maybe one little dot above the mouse cursor there.
How Bad is it Actually?
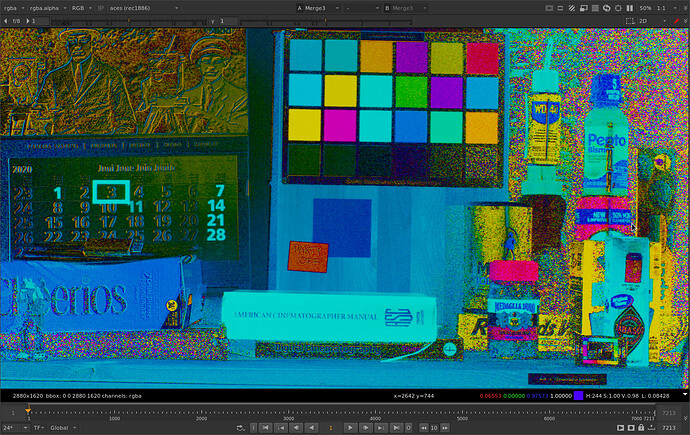
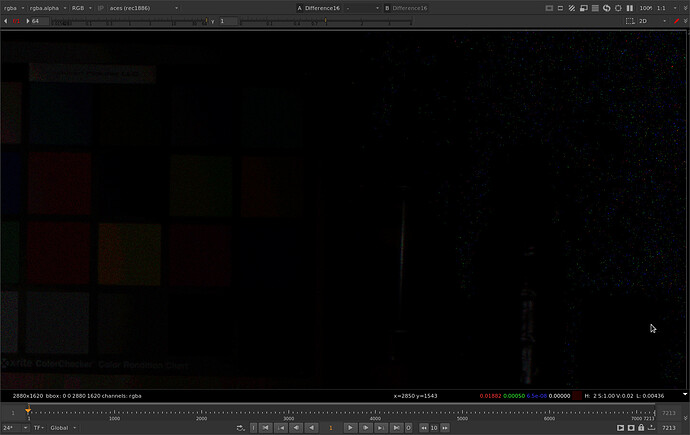
Not that bad. If you’re standards aren’t too high and you are looking for obvious differences, you probably won’t see a problem. But let’s look more closely because those pixels matter!
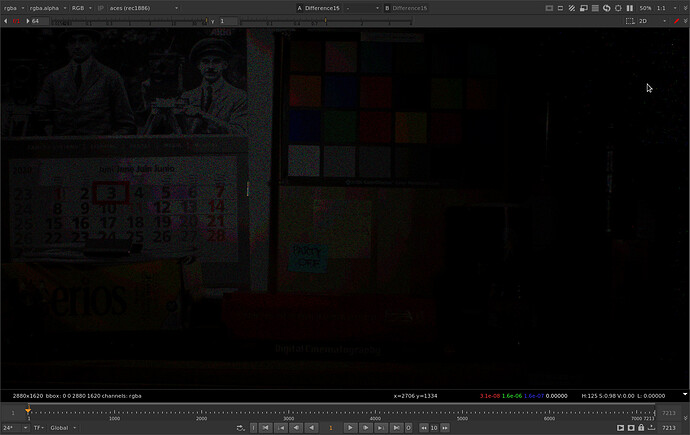
Let’s expose up so we can see what’s going on.
Cool so we have our familiar quantization errors from rendering as 16 bit half float. We also have a lot of speckly noise in the shadow grain. Let’s take a closer look.
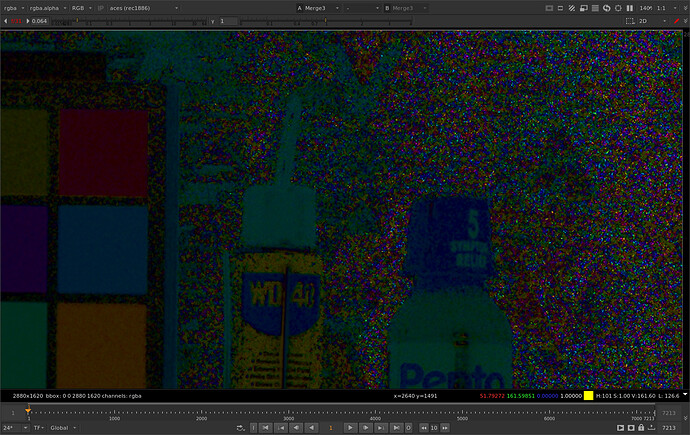
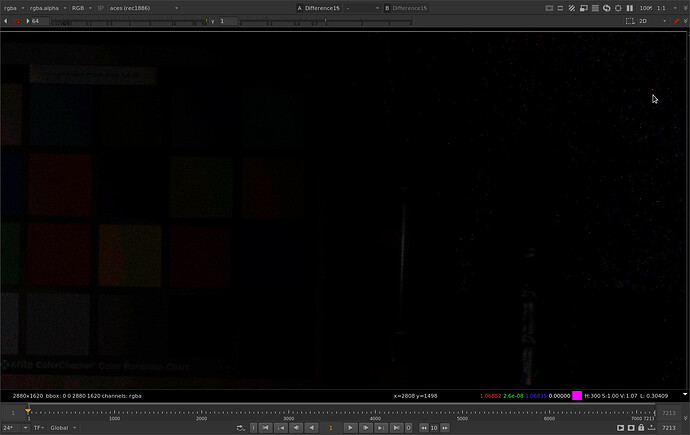
Zooming 1:1 we can see a bit more clearly that there are individual pixels that have pretty big differences. I’ve sampled one here that has a difference in the blue channel of 1.068. These differences are also noticeable because they are tied to the grain which is random on every frame.
Here is frame 2. You can imagine what that looks like in motion.
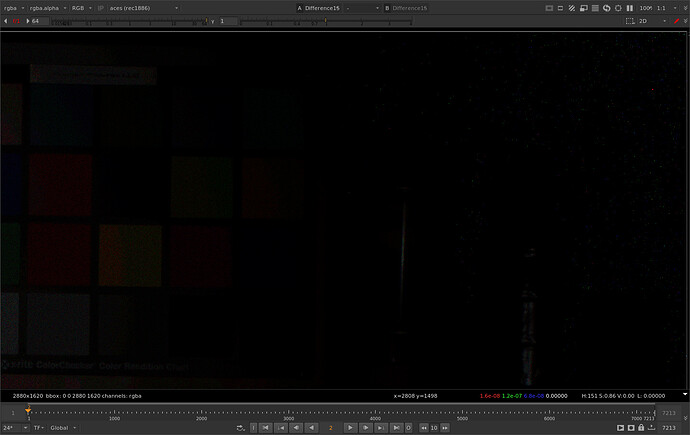
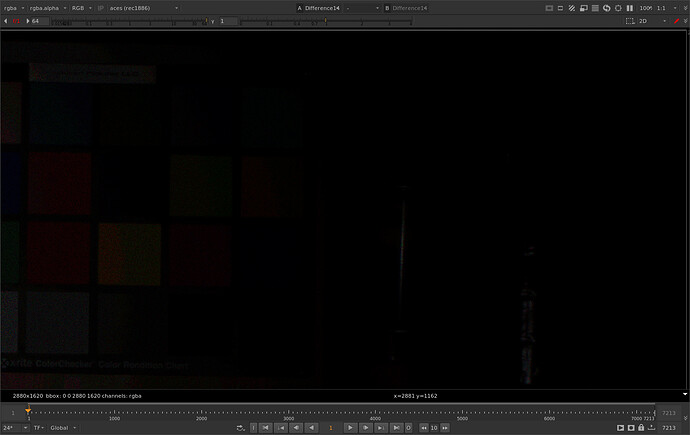
The situation gets more pronounced as the aggressiveness of the compression curve is increased. Here is with a power of 2.0 instead of the default of 1.2.
Here is with 1.2 power and a shadow rolloff of 0.02. Speckles are gone. Even a lower setting like 0.008 works very well.
Downside
Of course there is a downside. If shadow rolloff is enabled, the algorithm is not exposure invariant. If there is a color that is out of gamut that you care about below the shadow rolloff threshold, it will be affected less or not at all.
This means that it’s important for your images to be exposed well before gamut compression is applied.
Useful or Not?
I’ve decided to change the shadow rolloff default to off in the release v0.6, because I think the differences described above may only be relevant to a smaller subset of the possible users. The problems that it creates when an image is underexposed may outweigh the problem described above.
Hopefully this post helps to explain the problem and my thinking about the solution. Perhaps it will help someone in the future troubleshooting the same invertibility issue.