Hey Alex,
QQ: Are the AP0 colours gamut mapped before entering ZCAM?
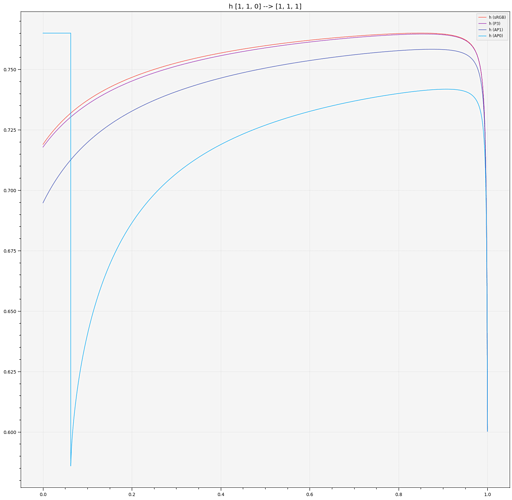
APO exhibit rather dramatic singularities, and the fact that its basis is rotated so much compared to usual colourspace probably does not help.
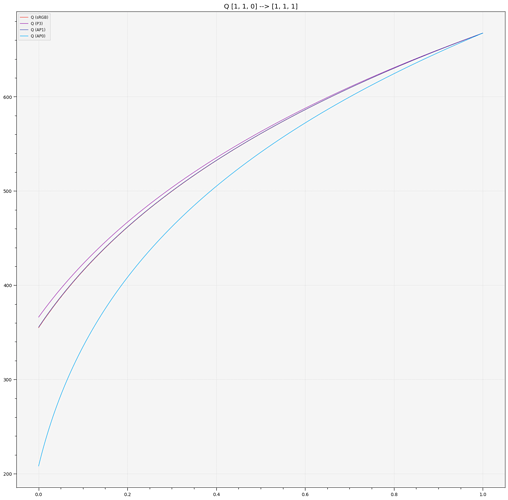
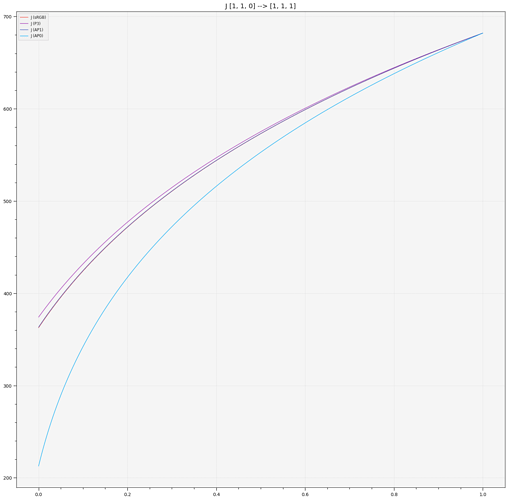
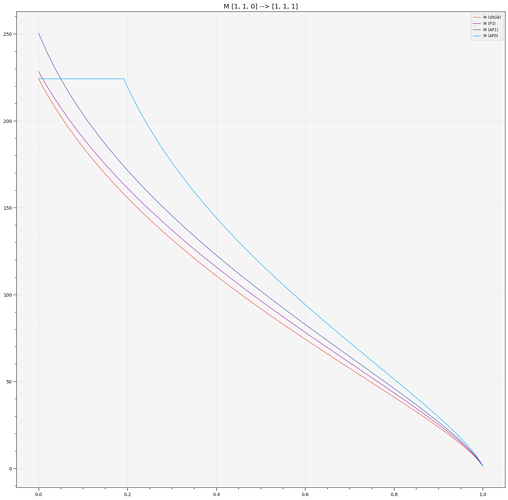
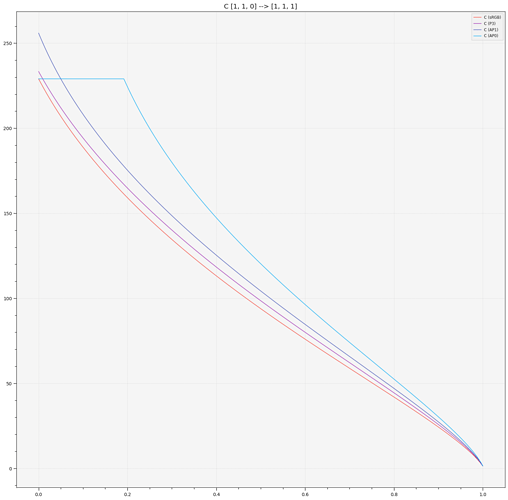
Blue to White Ramp and looking at the various correlates only (with AP0 correlates clipped to [-inf, max(sRGB Correlate)]):
The most interesting ones here are obviously, M, C and h, they point out that we cannot afford not gamut map before ZCAM, non-physically realisable colours are behaving in a rather unpredictable way.
Cheers,
Thomas