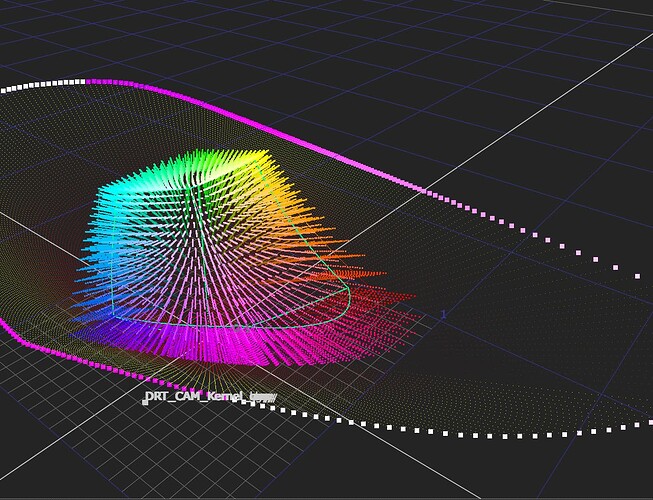
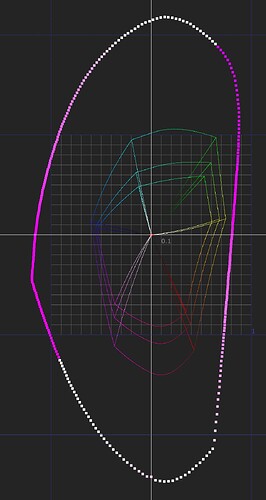
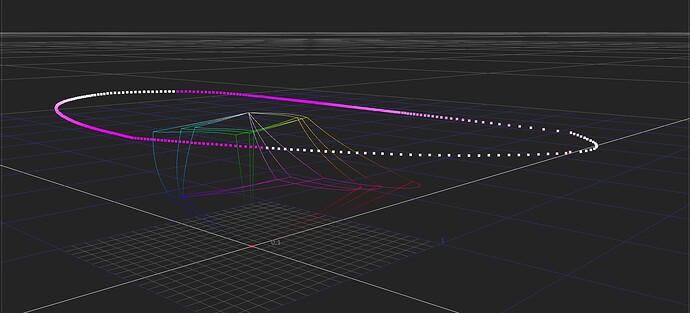
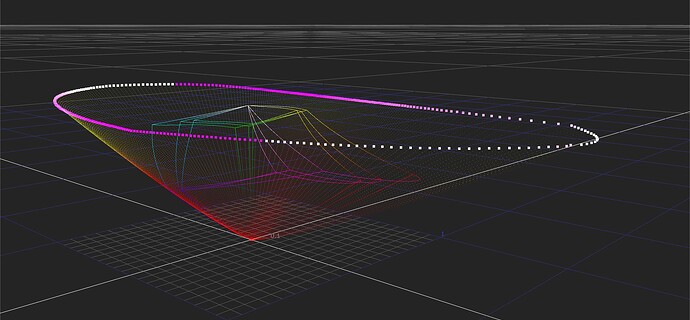
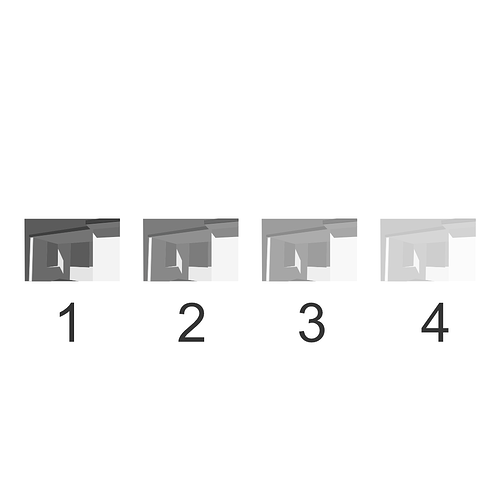Correct.
There appears a cognitive probability “heuristic” derived from the differentials that leads to some rather incredible effects. A good example is how our cognition “decomposes” various chromatic relationship fields into “meaning”. Some of the cognitive evidence appears to be gleaned from the underlying differential field relationships. While publicly available differential system mechanics are not well documented, we can at least consider luminance as a very loose approximation. Very loose because ultimately we cognitively derive “lightness” from the field relationships, hence no discrete measurement of anything gives us any indication of “colour” qualia.
100%.
This is probably a deeper issue than it appears at first blush given how sensitive we are to differential field relationships.
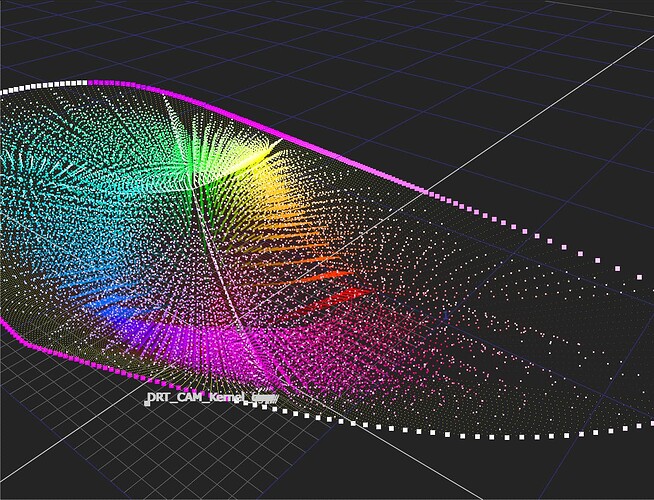
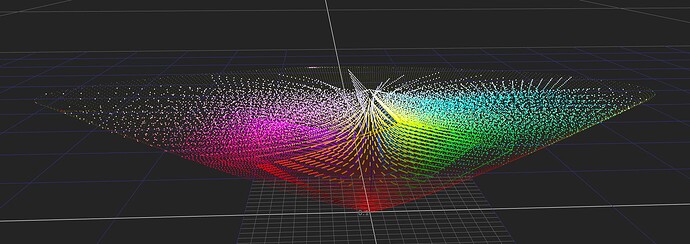
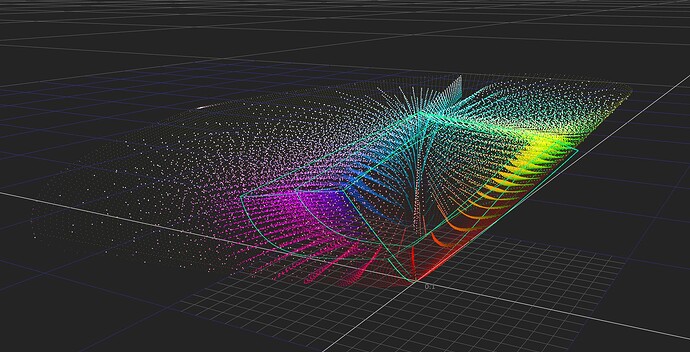
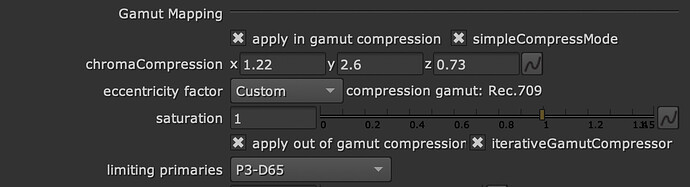
I am confident someone can design a Caplovitz-Tse1 or Anderson-Winawer2 inspired test that has layered transparency. I suspect it will reveal that as the exposure sweeps increase, the cognition of layered transparencies may fall apart. I farted around a little bit sampling from the “spectral” picture in an attempt to identify the cognitive pothole, and would suggest that the model is cross warping the “luminance” along the scale. For example, we can get a very real sense as to how sensitive our cognition is to the differentials between values. Making a swatch too pure can totally explode these relationships. The following shows partial spheres that are “null” R=G=B in each of the read “overlapped” regions. When the fields are of a certain differential, the cognition of layering and the underlying cascading cognition of chroma is different for each.
A tweak of the purities can completely blow up the picture-text.
TL;DR: Chasing higher purities by farting with the signal relationships can lead to weird picture grammar.
I don’t think it matters between the versions? I think the “model” and the picture forming mechanic is doubling up the neurophysiological signals.
That is, imagine for a moment we take BT.709 pure “blue” and evaluate along some “brightness” metric. For the sake of argument, let’s use “luminance” because it’s rather well defined. Now imagine we deduce that the luminance of the value at some emission is 0.0722 units. So we “map” this value, which would broadly be corresponding to the J mapping component. Knowing it’s low, we map it low.
The problem with this logic is that it’s a complete double up on what we are doing. The BT.709 “brightness” is only 0.0722 units when balanced for the neurophysiological energy stimulus of the stasis of the three channels of the medium. That is, it’s only 0.0722 units when we are at unit 1.0 relative to the complement, which means we ought to be mapping unit 1.0, not the “apparent brightness”. If we map the “brightness” down, we end up potentially mangling up the relationships.
In the most simple and basic terms, it is utterly illogical that, when balanced for an achromatic output, the higher luminance neurophysiological stimuli (EG: “Yellows”) are mapped to a lower luminance than the more powerful chromatic strength signals (EG: “Blues”). It is very clear that the chromatic strength, or chrominance, of a given stimulus, is inversely proportional to the relative luminance.
I’ve been trying to put my finger on why the pictures have some strange slewing happening with respect to the formed colour, and I can only suspect it is a result of this fundamentally flawed logic, and is reflected in some of the layering / transparency pictures I’ve experimented with. I’d be happy if someone were to suggest where this logic is incorrect.
It should be noted that both creative film and the more classic channel-by-channel curve approach happen to map the “energy”, and the cognitive impact related to chromatic strength of the colours is interwoven into the underlying models themselves. For example, when density layers in creative film are equal, following the Beer-Lamber-Bouguer law, the result is a “null” differential between the three dye layers in terms of cognition, aka “achromatic” in the broad field sense. This equal density equals achromatic holds along the totality of the density continuum.
Indeed, there’s no such “singular function” as per Sharpe et. al3, given that the “lightness” is determined by the spatiotemporal differential field, not discrete signal sample magnitude. It doesn’t really matter in our case as any weighting will hold the relationships uniformly.
This plausibly means that the broad luminance differential relationships are incredibly important in the formed picture. If we pooch the “order” through these sorts of oversights, we will end up with things that can cause cognitive dissonance to the reading of the picture-text.

—
1 Caplovitz, Gideon P, and Peter U Tse. “The Bar — Cross — Ellipse Illusion: Alternating Percepts of Rigid and Nonrigid Motion Based on Contour Ownership and Trackable Feature Assignment.” Perception 35, no. 7 (July 2006): 993–97. https://doi.org/10.1068/p5568.
2Anderson, Barton L., and Jonathan Winawer. “Layered Image Representations and the Computation of Surface Lightness.” Journal of Vision 8, no. 7 (July 7, 2008): 18. Layered image representations and the computation of surface lightness | JOV | ARVO Journals.
3Sharpe, Lindsay T., Andrew Stockman, Wolfgang Jagla, and Herbert Jägle. “A Luminous Efficiency Function, VD65* (λ), for Daylight Adaptation: A Correction.” Color Research & Application 36, no. 1 (February 2011): 42–46. https://doi.org/10.1002/col.20602.