Matrices
Unsure.
I’ve tried with sum to unity matrices and the results still shift, Illuminant E for example. The coefficients aren’t constrained enough it seems, and I’m unsure how to constrain them. I think it would require a constraint between Y and X to Z? Unsure, but would be interested to hear ideas. If I were to speculate as to the “why”, my best guess is that the neurophysiological differential signal, in the “fixed” case of the Standard Observer model is entwined into the three XYZ Cartesian coordinates. More specifically, given an attempt was made to isolate the P+D via the Y component of XYZ, the remaining vector is buried in X and Z. This is just pure speculation of course, with a degree of evidence to support that claim. TL;DR: I am unsure a 3x3 matrix, with only two degrees of freedom in a three dimensional Cartesian projection can supply enough control?
Chrominance
Chrominance ConspiracyTheory.GIF from the Arkham Sanitarium
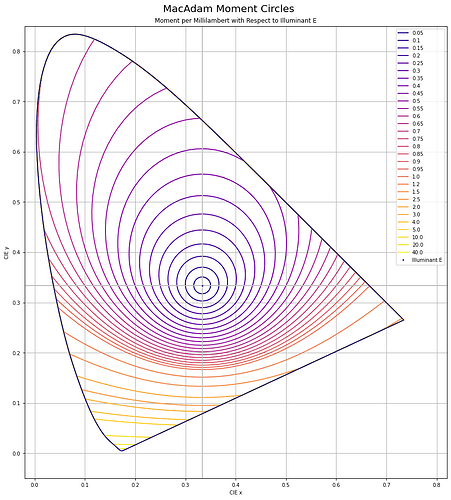
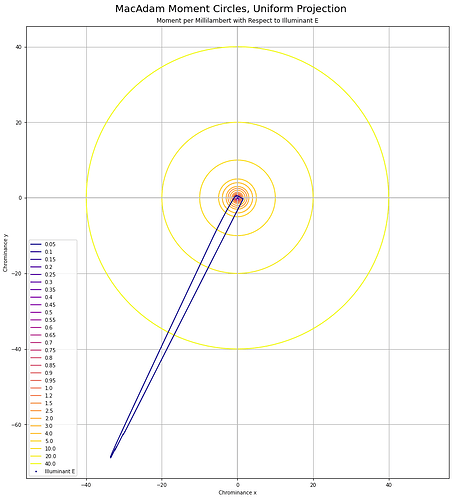
Chrominance follows the MacAdam work. I’ve recreated the original MacAdam diagram using a “uniform projection” space, and sampling concentric circles, then reprojected back to CIE xy:
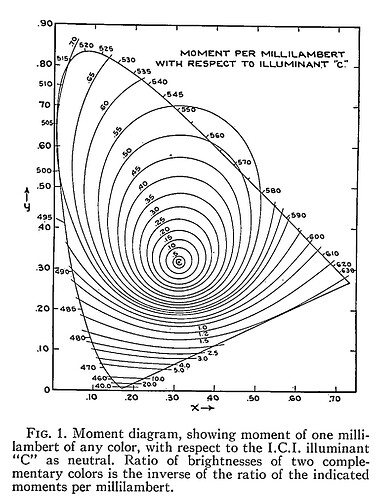
Here is the original diagram1 I was seeking to replicate:
We can calculate the ratios for any colinear CIE xy chromaticity through any arbitrary coordinate using a projection into a uniform vector space. It’s easiest to think of chrominance as the magnitude vector that forms from relative X to Z. Y remains isolated.
Oddly, I was unable to find any papers that cited the reprojection to a “uniform chrominance” projection. That projection looks like this when using the 1931 Observer system:
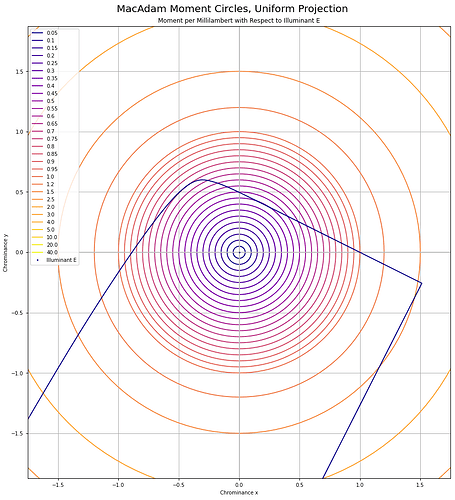
It can be useful to think of chrominance as the X to Z plane, with Y divided out to form an equi-energy projection. Here are the MacAdam “Moment” elliptical shapes, when projected into this equi-chrominance projection, cropped for clarity:
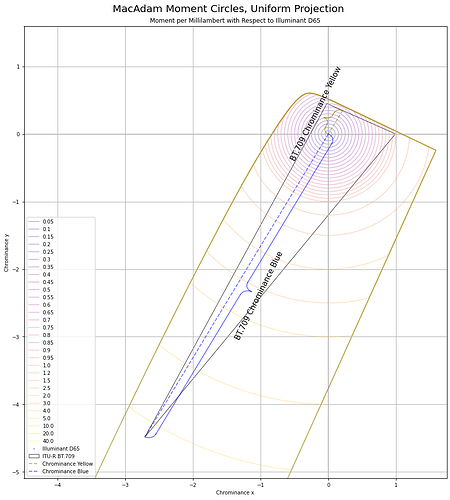
And here’s BT.709 projected into this chrominance plane:
The final “ratios” of underlying current stimulus are derived from the simple Euclidean distance ratios, which given they are ratios, plausibly is a direct line to the underlying differentials:
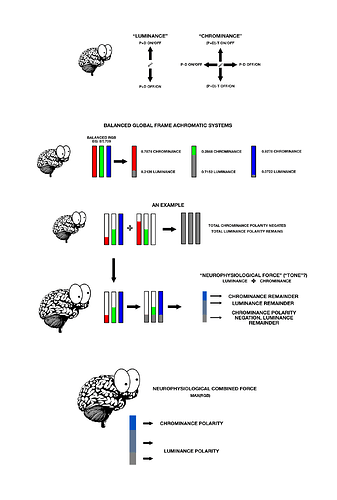
If we wander down this path of nonsense, total “neurophysiological” influence is the combined force of the resultant neurophysiological differentials, where “differentials” are not only the differences of the absorptive profiles, but the On-Off and Off-On assemblies:
- The (P+D) signal can be broadly considered {Y}.
- The combined vector magnitude of the (P-D) and (P+D)-T signal path is entwined in X to Z.
This means we should be able to calculate the ratios of gains of energy required to hit the target global frame achromatic using the ratios of either Y or the X to Z magnitudes. Using the projection above, the total Euclidean distance of the chrominance vectors is 5.239601 + 0.407705, for a total of 5.647306. If we divide each vector magnitude by the sum, we end up with the two cases for BT.709 “blue” and “yellow”:
0.407705 / 5.647306 which yields 0.07219460039.5.239601 / 5.647306 which yields 0.9278053996.
If those resulting ratio values look awfully familiar to folks, they should. Those happen to be the luminance weights of BT.709 “blue” and “yellow” respectively.
Incriminating Evidence against CAMs and UCSs
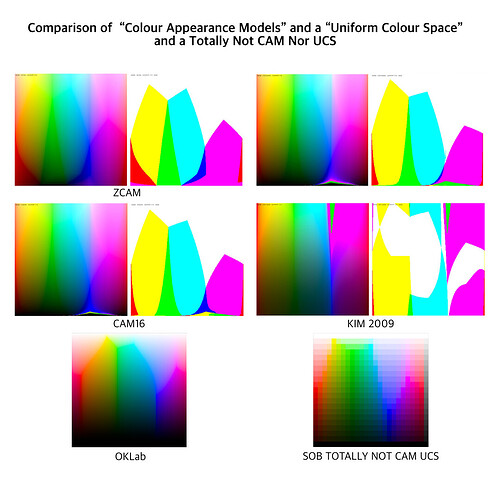
Moving along, if we consider literally all of the Colour Appearance Models and Uniform Colour Space attempts that have been made over the past half of a century, a peculiar trend line follows out of them. Let’s take a look by way of a post here on the forum, cropped, flipped, and collated against a Uniform Colour Model, and a Totally Not CAM / UCS Model from Yours Truly. The “model” I generated was simply a pure luminance mapping, with attenuation of purity to hit the target luminance, such as when a given luminance was unachievable at the mapping peg position. Note how all of the “clefts” in the CAMs match the exact clefts in the UCS, which in turn match the exact clefts in the luminance mapper:
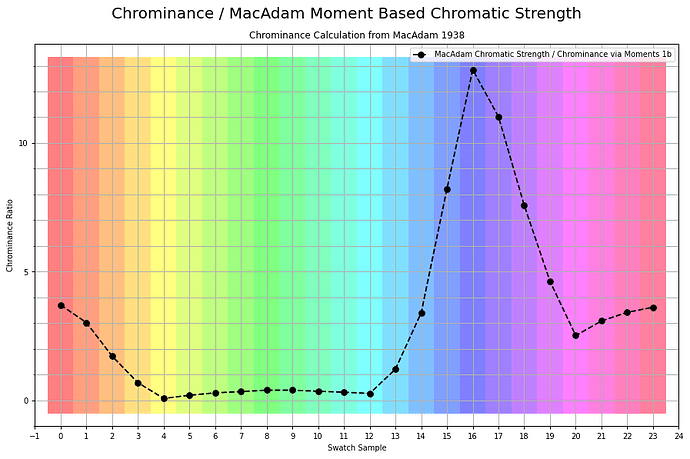
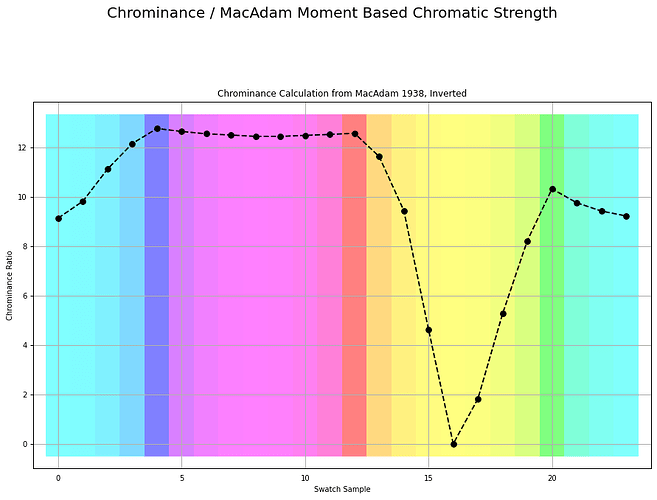
If we were to plot the chrominance ratios for a similar sweep of tristimulus using BT.709, it looks like this:
Here is the exact same measurement, inverted as over complementary values that accumulate to the achromatic Grassmann middle:
I believe it was Luke who, in the most recent meeting, stated:
The relationship between linear light and J is different than the relationship between linear light and M.
If we correct for that pattern, by way of gaining the underlying magnitudes of the tristimulus, I’ll leave it up to the reader to speculate with a wild guess as to what model we end up with if we were to indeed yield constant relationships between the chrominance ratio and the luminance ratio. Here is a passage of an example of the stated problem from the MacAdam original work:
Figure 1 can be used to advantage in any problem in which a neutral additive mixture is to be established. If, for instance, it is necessary to secure a white image on the screen in connection with an additive method of projection of colored photographs, suitable relative brightnesses of the three projection primaries can be readily determined.
Chrominance: The Shortcut
Given we are already often in balanced systems, working through the values from the Standard Observer has a direct shortcut. Chrominance is to Luminance as:
- Luminance =
(R_w * R) + (G_w * G) + (B_w * B)
- Chrominance =
max(RGB) - Luminance(RGB)
If that happens to look all too convenient, it is because RGB is already engineered to be a balanced system, and the underlying “force” gains are baked into the model. To recover the magnitude we just have to “extract” it.
Note the definition of chrominance here is following the one outlined by Boynton2, and is congruent with the other definitions such as those of Chromatic Strength, Complementation Valence, from folks such as Evans and Swenholt, Hurvich and Jameson, and Sinden:
We are now in a position to define a new term: chrominance. Whereas luminance refers to a weighted measure of stimulus energy, which takes into account the spectral sensitivity of the eye to brightness, chrominance refers to a weighted measure of stimulus energy, which takes into account the spectral sensitivity of the eye to color.
The simple description is that vector magnitude between X to Z.
—
1 MacAdam, David L. “Photometric Relationships Between Complementary Colors*.” Journal of the Optical Society of America 28, no. 4 (April 1, 1938): 103. Photometric Relationships Between Complementary Colors*.
2Boynton, Robert M. “Theory of Color Vision.” Journal of the Optical Society of America 50, no. 10 (October 1, 1960): 929. Theory of Color Vision.