I have been working a bit on parameterization since my last post, Trying to figure out a robust and simple model for how the different parameters change with different display outputs.
I have settled on a set of parameters which I think are pretty simple and work pretty well, even for HDR.
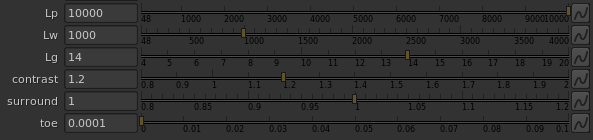
- Lp - Peak display luminance in nits. Used for HDR output, when peak white and peak luminance of the inverse EOTF container might not match. For example for ST-2084 PQ rendering, Lp will be 10,000 and Lw might be some other value.
- Lw - White luminance in nits. In SDR, Lw and Lp would probably be equal.
- Lg - Grey luminance in nits.
- Contrast - a constrained contrast control which pivots around the output middle grey value.
- Surround - an unconstrained power function adjustment for surround luminance adjustment.
- Toe - a parabolic toe compression for flare compensation.
There is then a layer of calculations which calculates static values based on the above parameter set:

-
p = Final power function parameter. Equal to
Contrast * Surround -
grey - Input → Output grey mapping. Output grey value equal to
Lg / Lp - w - Input exposure adjustment. Calculates a scale factor such that input grey maps to output grey through the compression functions.
-
w_hdr - Boost input exposure by some amount when Lw > 1000 nits. I have calculated it here as
max(1,pow(Lw/1000,0.1)), but this could be creatively adjusted. (This paramete is not pictured above, as it is included in the scale). -
h - Simple linear model which adjusts output domain scale such that clip occurs at some finite input domain value. This varies with Lw:
0.048*Lw/1000+1.037is what I came up with, but it could be adjusted creatively. -
scale - Final input and output domain scales:
scale.x = w * w_hdr,
scale.y = Lw / Lp * h
Here are two compression functions using this parameterization. The first is based on @daniele 's formulation, but with some modifications so that input domain scale happens first and output domain scale happens last:
Tonemap_ToeLast_v1.1.nk (3.3 KB)
The second is a simpler version of my piecewise hyperbolic compression function with the white intersection constraint removed, because it is no longer necessary with this parameterization.
Tonemap_PiecewiseHyperbolic_v3.nk (4.0 KB)
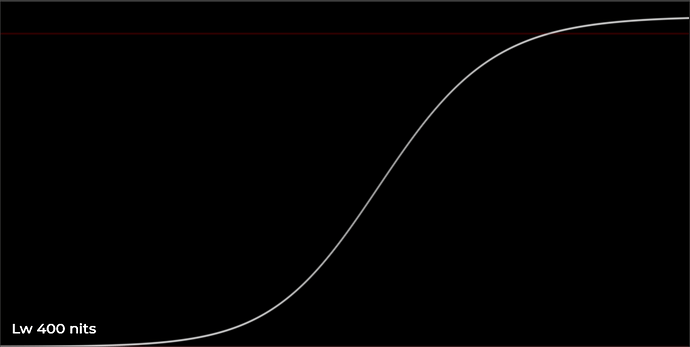
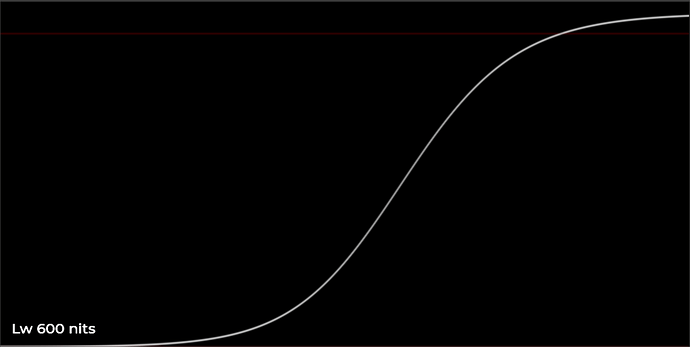
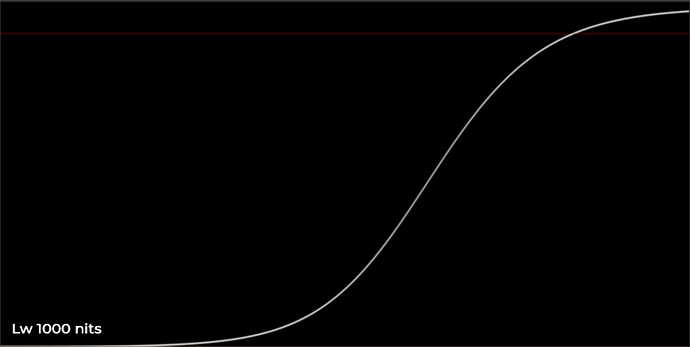
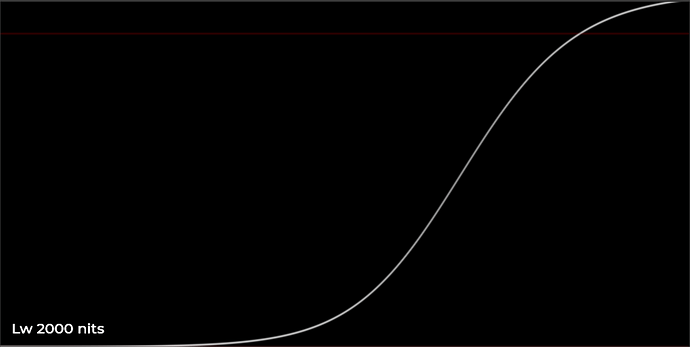
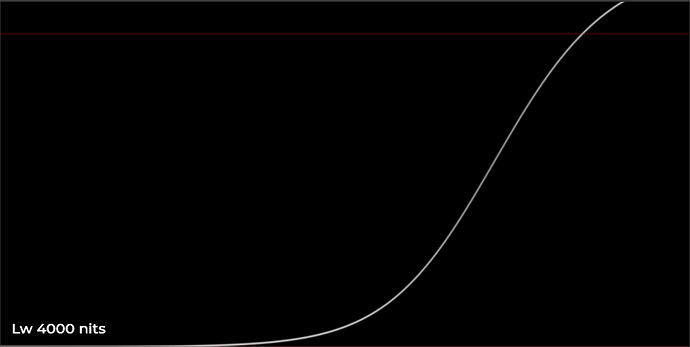
Here are a few plots showing the behavior of the HDR curve with varying values of Lw, through the piecewise hyperbolic curve. The input is an exponential input ramp, ranging from 5 stops below 0.18 to 12 stops above 0.18. This lets us see a log-ranging x-axis in the plot. Note that in these plots I have removed the output scale which normalizes Lw to the correct position in the PQ container, so that we can see peak white at 1.0 for all curves in order to compare them effectively.