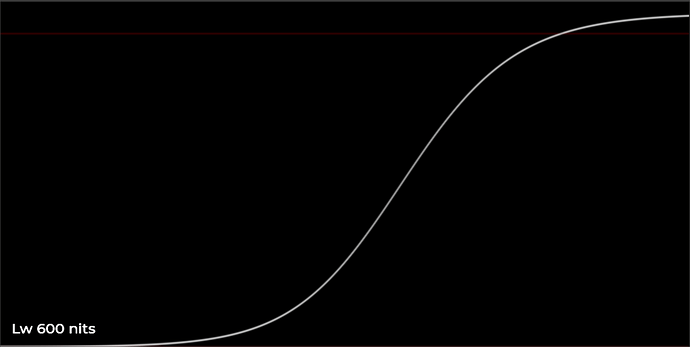
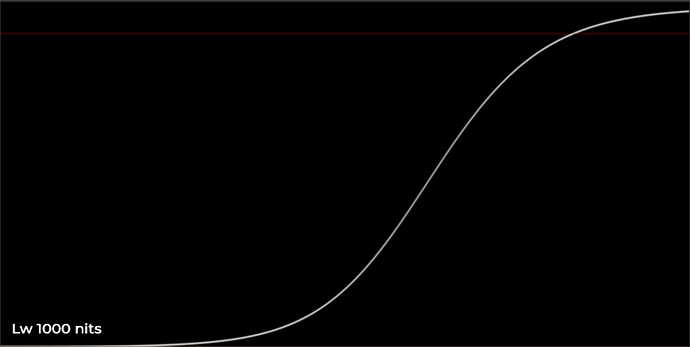
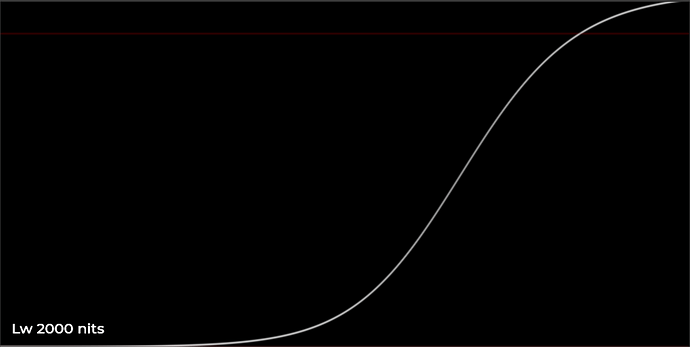
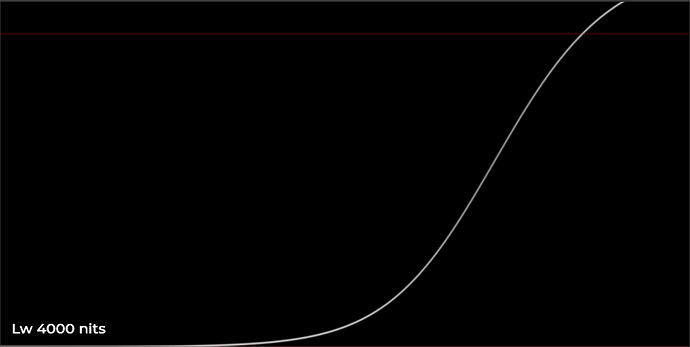
Further Simplification of the Parameter Model
I spent some time doing further work on the parameter model. My goal is to figure out a simple elegant behavior for the curve control parameters in terms of display luminance Lw, in order to create a model that smoothly transitions from SDR to HDR.
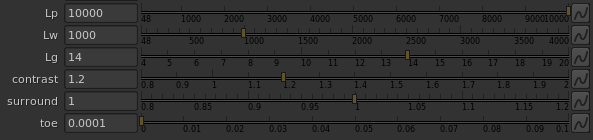
Previously I had a control w for boosting exposure with HDR peak luminance like @daniele mentioned in one of the previous meetings. I wondered if this idea could be extended to a simple model for changing grey nit level Lg based on peak white luminance Lw. Maybe something that would work across all values of Lw from 100 nits to 4000 nits.
I gathered some sample values, looked at the behavior, and used the desmos regression solver to come up with a simple log function which models it pretty well. This could of course be altered depending on rendering or aesthetic preferences.
L_{g}=14.4+1.436\ \ln\left(\frac{L_{w}}{1000}\right)
The result sets the middle grey value based on Lw pretty effectively.
Doing the same thing for the toe flare/glare compensation control: t_{0}=\frac{1}{L_{w}} seems to be a very good fit to the observed behavior of how the amount of toe compensation should be reduced as peak luminance increases.
All of this should be further refined and validated with testing of course, but the behavior seems to work quite well with the limited consumer-level display devices which I have at my disposal.
Experiment Time
Most LCD computer monitors these days can output 250 nits or more. Yet if we are calibrating to Rec.709, we set the luminance to 100 nits.
For a long time I’ve wondered if it were possible and what it would look like to render an image for proper display on a monitor with a higher nit level. Using the model described above I decided to finally do just such an experiment. I’ll share the results here because I think they are pretty interesting and do a good job of showing the visual difference between hdr and sdr in a relative way.
Experiment Summary
I have two computer monitors:
- HP Dreamcolor Z27x G2
- DELL U2713HM
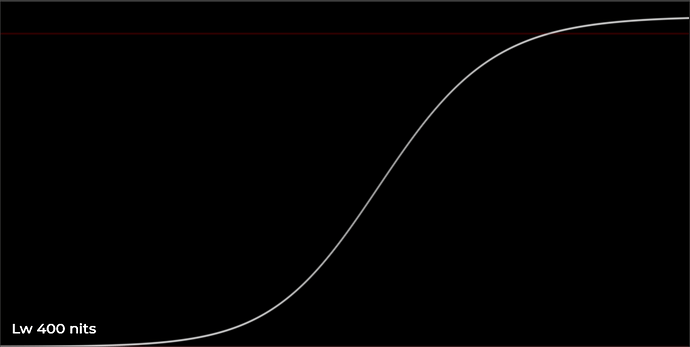
I set my Dell to be 100 nits and my HP to be 250 nits. Using OpenDRT_v0.0.81b3, I rendered one image using Lw = 100 nits, and one using Lw = 250 nits and put them on their respective monitors.
I was surprised that their appearance actually looked pretty similar, after my eyes adjusted. The 250 nit version had more range and clarity in the highlights and shadows, and the 100 nit version looked a bit more dull and compressed. Once my eyes adapted to each image though, their appearance was very similar. We can do a variation of this comparison using only one SDR monitor with the luminance cranked up as far as it will go. By rendering one image with a peak white of some value, say 250 nit or 600 nit, and the other image with a 100 nit white luminance, but a peak luminance matching the 250 nit or 600 nit output (this can be achieved by overriding the Lp setting in the OpenDRT node).
I’ll include a couple of comparison images below. To view them, crank up your monitor brightness as high as it will go and view the images full screen with no UI visible, and do the comparison in a dark room with the lights off. Also if you have something like a piece of black foam-core to cover the image you are not viewing, it will help you get a more accurate perception.
On the top is an image scaled to simulate a 100 nit output on a 250 nit monitor: Lw = 100, Lp = 250.
On the bottom is the same image rendered at the full 250 nits: Lw = 250, Lp = 250.
I’ve uploaded more of these test images here:
https://mega.nz/folder/zmQFGYIQ#QBi5RkfFfaCdV4rfc06_hA
The same experiment could be performed to compare a 600 nit rendering to a 100 nit rendering, though maybe less precise without access to a proper HDR display.
And all the same images but vs.600 nit available here:
https://mega.nz/folder/XzZHiaTI#CT3VbT94pg-BHxEkafJlGg
And here is the nuke script I used to generate all these test images.
opendrt_100nit_vs_hdr.nk (193.2 KB)
The source images are from the ODT VWG, the Gamut Mapping VWG and the VMLab Stuttgart HDR Test Images, and a few beautiful CG Renders by @ChrisBrejon (Hopefully he doesn’t mind me using them here).
With the increase in “VESA Display HDR 400” monitors, I think this experiment is particularly relevant today.
I’m somewhat confident I’ve set all of this up correctly, but if any of you smart people see any errors feel free to point them out!