I went back to @daniele’s original post and took another pass at understanding it.
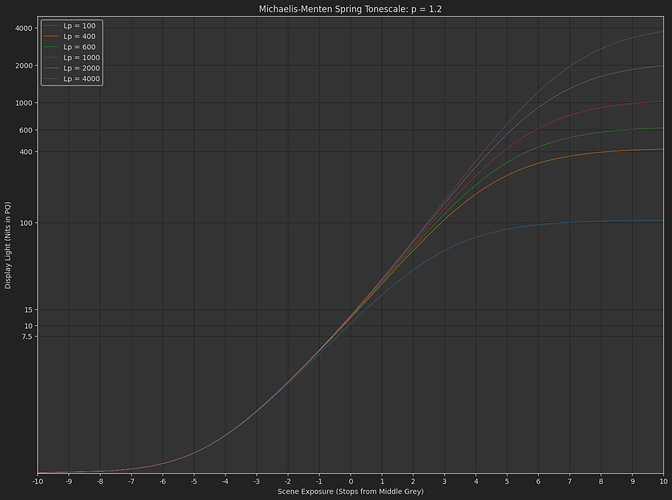
One thing I noticed making the naka-rushton model above (and many times in the many garbage dead-end post I did before) is that with an intersection constraint at grey, it’s very easy to get undesireable behavior in the low end below the constraint. Slope changes or contrast changes, “wobbling” as you do tweaks of the curves for different peak luminance outputs.
The really cool thing about Daniele’s original formulation is that it is very stable down there. (Why am I am only fully appreciating this now nearly a year later  )
)
The reason it is stable is because in simple terms if you have
f\left(x\right)=s_{1}\frac{x}{x+s_{1}}
The bottom end is very stable as you adjust s_1
If you add a power function
f\left(x\right)=s_{1}\left(\frac{x}{x+s_{0}}\right)^{p}
where s_{0}=e_{0}s_{1}^{\frac{1}{p}}
The bottom end is still very stable, and we have control over scene-referred exposure e_0 and “contrast” p.
This can give very controllable and predicable results actually.
Here’s another desmos comparing this function with the naka-rushton one, with s_0 normalized in the same way. It’s pretty clear the different behavior of the exponent between the two curves.