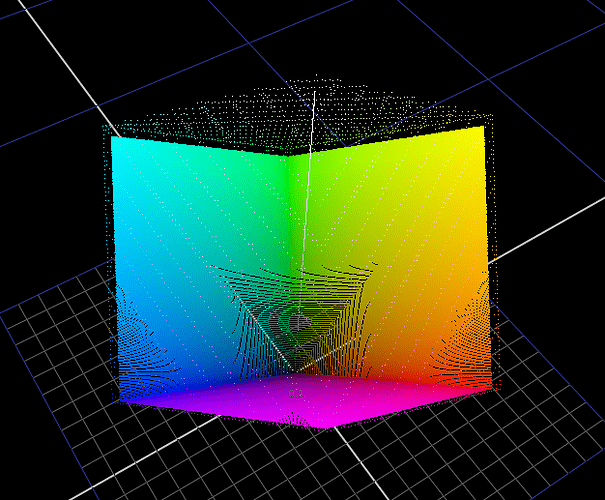
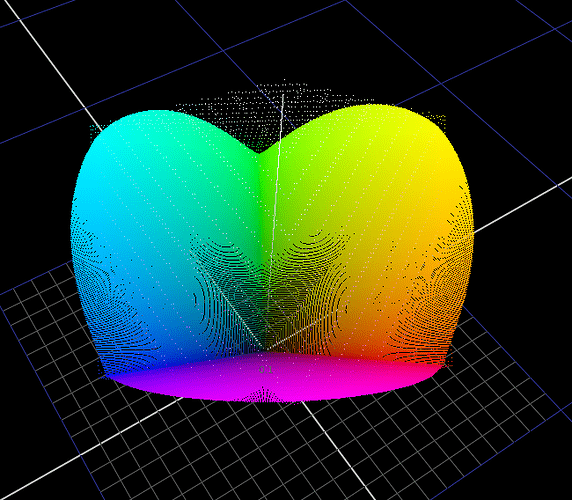
Norms
To visualize what different norms are actually doing I’ve found it useful to plot hue sweeps.
MaxRGB keeps it’s shape.
Vector Length / Euclidean distance forms a smooth curve through the secondaries but the cusp at the primaries sharp.
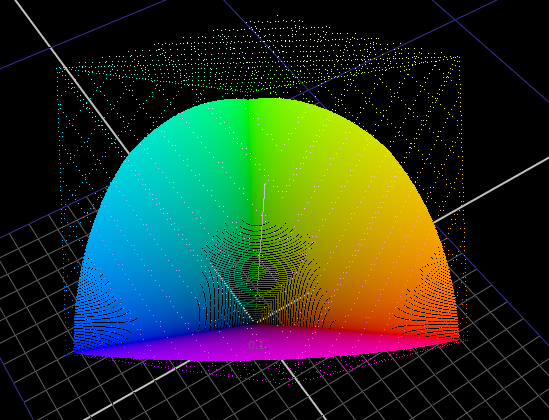
Power norm is pretty wonky and really depends on what power you use. This is with 2.38

And sweeps in the same order:
Here’s a nuke setup with a bunch of norms and the sweep if anyone wants to play.
plot_norm_sweep.nk (20.6 KB)
Updated ToneCompress Formulation
I found the intersection constraints and behavior in my last post to be a bit inelegant. I kept working on the problem and I’ve come up with something which I think is better.
ToneCompress_v3.nk (4.1 KB)
Changes
I’ve made a couple of changes to my previous approach.
- Move toe/flare adjustment before shoulder compression in order to avoid changing peak white intersection. This simplifies a lot the calculations for the peak white intersection constraint.
- Simplify parameters a bit.
- Remove constraint on output domain scale. This lets us scale the whole curve. This will change middle grey though. Curious to hear thoughts on this. Is it okay for mid-grey intersection constraint to be altered when adjusting output domain scale?
- Change shoulder compression function to a piecewise hyperbolic curve with linear section. After a bunch of experimenting, I’ve decided that I like the look of keeping a linear section in the shoulder compression. There is a bit more… skin sparkle.
Here are a couple of pictures to show what I mean.