Given I brought up the point in the last meeting, and given several birdies have asked that I post the question here, I figured I’d bump up the recent revival of this thread.
First, a salient quote from Jed Smith:
Even in this valuable post of Jed’s there is an implicit assumption of what “tone” is. These sorts of a priori assumptions will doom any attempt at modelling. What is this particular version of “tone”?
Further down this ladder, I’d like to highlight a quote that @Alexander_Forsythe made in Slack, when I, being a buffoon, kept repeating the question “What is tone?”
I’ll have to look in the usual places to see if it’s already defined but I’ll take a shot off the top of my head. Take with a grain of salt.
Tone mapping: the intentional modification of the relationship between relative scene luminance values and display luminance values usually intended to compensate for limitations in minimum and maximum achievable luminance levels of a particular display, perceptual effects associated with viewing environment differences between the scene and the reproduction, and preferential image reproduction characteristics. Tone mapping may be achieved through a variety of means but is quantified by its net effect on relationship between relative scene luminance values and display luminance values.
That is, if this definition of “tone” is acceptable, does anything that uses the term “tone” (EG: “tone mapping”, “Simple Stage Tone Scale”) actually perform the implied mechanic? Does a “tone map” actually “map tones”?
None of the functional formula examples thus far map “tones” according to this definition. Either this should be considered a show stopper, or further interrogation is required.
Given the above, if we revisit this issue cited by Forsythe, we can ask some further questions…
A few questions:
- Is there a conflation between chroma and tone in some of these nuanced discussions?
- If there is, how are the two related?
- If there is a relationship, can anyone answer, in a clear statement, what “Film magic” did regarding tone, and this nuanced interaction?
- Given tone’s importance here, and specifically the “shape” of classical film negative to print to print through resultant density, is everyone confident in the evaluation of film density plots being 100% correlated to emission of light from a fixed chromaticity display?
- If not, is it feasible to consider how film density plots correlate to light transmission?
- Further along, is the correlation between film dye density and transmission related to discussions of chroma, as per Forsythe’s question?
TL;DR: Perhaps we should be avoiding discussions of “bleaching” or “desaturation” and interrogate precisely what film was doing, and more importantly, what underlying perceptual (?) mechanic was it facilitating that makes the rendition of imagery successful in the medium, and how is it related to “tonality”? With respect to gamut mapping “tones”, the underlying definitions and potential mechanics should be clearly identified to evaluate whether or not any mechanic is actually doing what it purports to achieve?
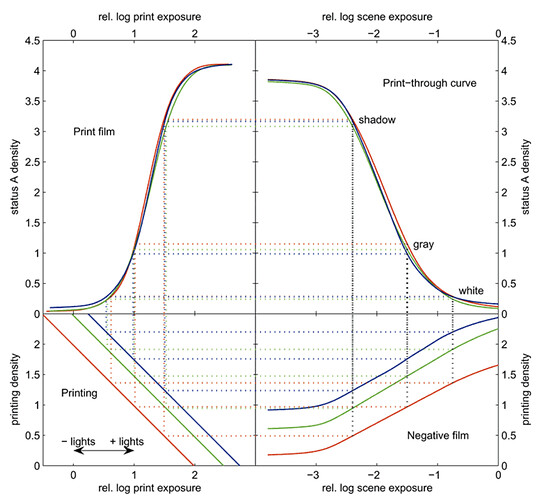
A while back @Alexander_Forsythe suggested it would be wise to include a discussion of a Jone’s Diagram such as the following. It seems related to this discussion, and why the “s” curve is even a part of the discussion around “tonality”.
Image from here.
Apologies to anyone who feels this is pedantry. From my dumbass vantage, I cannot see how we can solve any design problem without firmly locating what the problem is, in clear and precise terms. Even given the large amount of discussion on this subject thus far, I’m unconvinced we have definitions clear enough to write any algorithm for.