Hi.
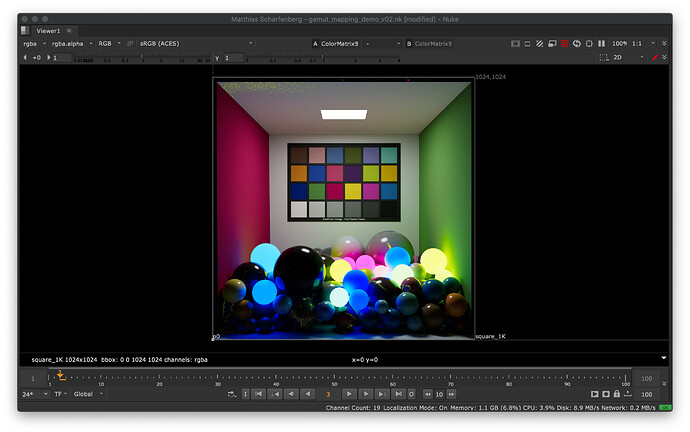
As mentioned during Meeting #6 and demo’ed at Meeting #7 I’m sharing a Nuke script illustrating some examples of simplistic approaches to the gamut mapping problem.
These are not intended as actual proposals, but rather to illustrate known issues and potential ideas for solutions.
So this is mainly meant as a conversation starter and an easy way for participants to look at some actual images.
The methods shown try to satisfy the following requirements for the algorithm:
- non-iterative
- exposure invariant
- source gamut agnostic
- adjustable core “confidence” gamut
The Nuke script does not rely on any custom plug-ins or external resources, except the images you want to try it out with.
It is (hopefully) self-explanatory enough to get everyone started, but please reach out with any problems or questions in using it.
Below is a quick explanation of the 6 mapping methods available in the script:
1. Unmapped:
No gamut mapping is being applied.
2. HSV Saturation Soft-Clip:
The image is converted to a cylindrical HSV projection of the target gamut and the saturation component is soft-clipped to 1.0.
Pros: extreme simplicity
Cons: significant over-compression, especially for red-yellow colours
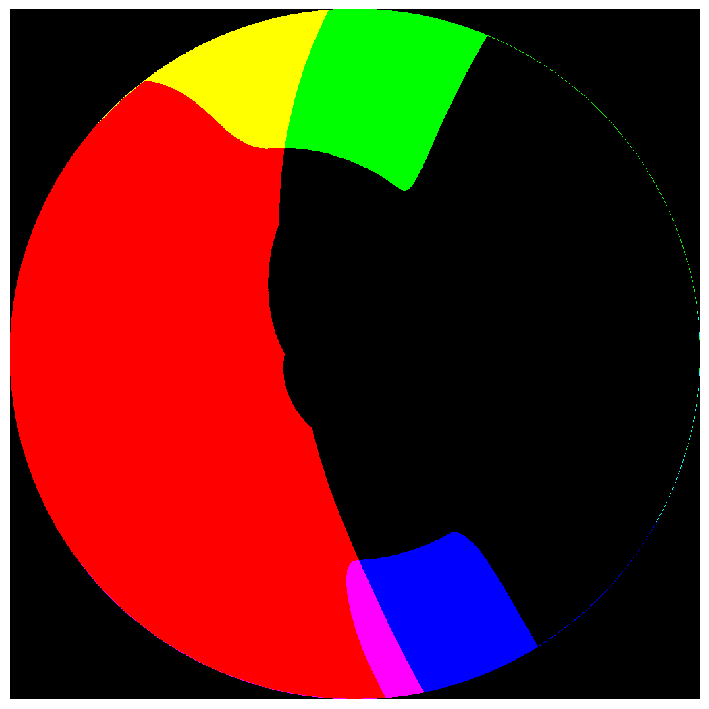
3. Soft-Project x,y:
The image is converted to CIE Yxy and the chromaticity coordinate is projected onto the target gamut boundary using a soft clip function on the distance from the white coordinate
Pros: simple and intuitive?
Cons: The luminance (Y) component is zero or negative for saturated blue colours and results in target gamut RGB values that are too dark or even black.
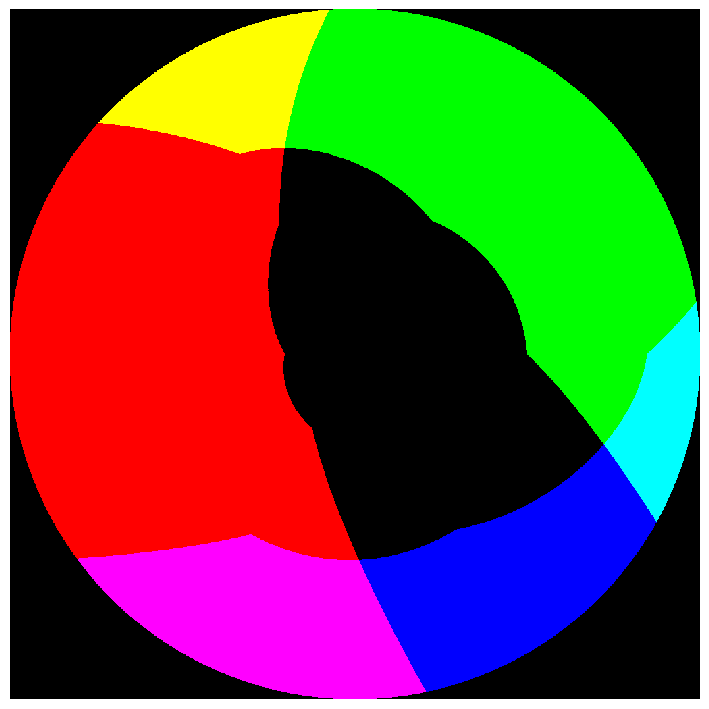
4. Normalized HSV Saturation Softclip in XYZ:
The image is converted to a cylindrical HSV projection of CIE XYZ. The saturation component is normalized to the boundary of the target gamut and then soft-clipped to 1.0.
Pros: relatively simple, does not suffer from the negative luminance issue of method #3
Cons: significant blue>purple “Abney Effect”, plot shows jagged non-monotonic mapping at target gamut boundary
5. Normalized HSV Saturation Softclip in LMS:
The image is converted to a cylindrical HSV projection of LMS cone fundamentals according to M. Safdar 2017. The saturation component is normalized to the boundary of the target gamut and then soft-clipped to 1.0.
Pros: also does not suffer from the negative luminance issue of method #3, M. Safdar cone fundamentals are supposed to suppress the shift to purple (although it doesn’t seem to have much effect in this example)
Cons: still significant blue>purple “Abney Effect”
6. Normalized HSV Saturation Softclip in LMS + purple suppression:
Like method #5 but also includes a pre-process step that slightly warps blue hue values to suppress the blue>purple “Abney Effect”. Distortion parameters were manually chosen for optimal visual results with available sample images.
Pros: much better mapping result for saturated blue colours
Cons: hue distortion does also affect colours within the “core gamut” and limiting it to the mapping region only results in counterintuitive hue shifts along saturation gradients
I look forward to hearing your feedback, suggestions and other examples.
Best Regards,
Matthias