Hi everyone!
I was chatting a bit with Chris Brejon, and he thought it would be useful if I shared some reflections and experiments I have done here. For those who don’t know me, my background is in video games and I guess my biggest claim to fame is having made Oklab, which I have seen pop up a few times in discussion here. I have never really worked with any part of ACES except for the output transforms, so my knowledge is a bit lacking regarding how it fits into the bigger picture.
This surely ended up being a lot of text and certainly more than I initially anticipated! I hope you found this interesting and relevant and that this post gives some fresh perspective and some new insights. Some of it has certainly been said before here, but hopefully most of it is new or different enough.
The post is split into three topics:
- Dealing with the sharp edges and corners of RGB gamuts
- Finding a path to white
- Input gamuts
Dealing with the sharp edges and corners of RGB gamuts
The shape of RGB gamuts form transformed cubes in linear color spaces (and some kind of distorted cubes in perceptual models). A consequence of this is that of you plot the hull of an RGB, you will not get smoothly varying colors.
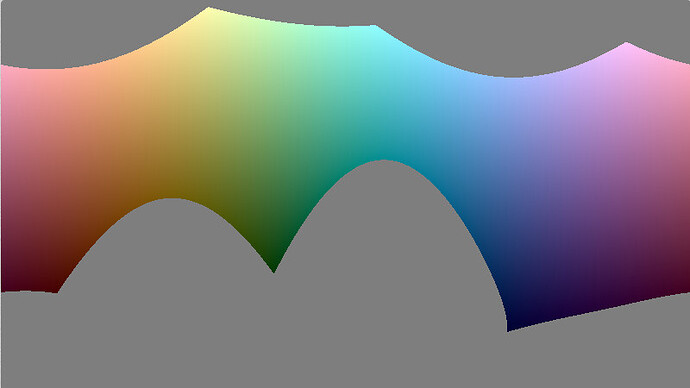
Here is a simple unwrap of linear sRGB:
The edges of the RGB volume are clearly visible as lines, meeting up at the RGB primaries and cyan, magenta and yellow.
This uneven shape poses a problem when doing gamut compression to RGB color spaces, at least if the mapping is required to reach all colors in the gamut. You end up in a situation where some smooth line in the input gamut is mapped the hull of the target RGB gamut, making the output non-smooth wherever the edges of the cubes are crossed.
This problem is unfortunately even worse if doing projections along constant hue and lightness lines. The reason is that the faces of the RGB cube end up almost perpendicular to hue and lightness in certain cases. This is most apparent in the transition from blue to cyan. You can clearly see it in this plot. Here in Oklab, but all models matching perception of hue will have this issue, since it is a property of hue perception.
So, what are the options for dealing with this when doing gamut compression?
1. Prioritize keeping hue and lightness* constant, and accept the uneven mapping at the boundary. You can, with a lot of effort, create a mapping where this does not affect the interior of the mapping. Okhsl is an example of this, mapping sRGB to a cylinder, but it does not fix the boundary. These methods are also fairly expensive to compute, since they require computing intersections between a line and the distorted RGB cube.
2. Keep hue and lightness* constant, but give up the requirement be able to reach all colors in the target gamut. This way you can smoothen the corners of the cube to get a smaller but smooth gamut.
3. Accept hue and lightness* distortions for very saturated colors. Make a transform that distorts hue and lightness* of saturated colors to move closer to the edges and corners of the RGB cube. In a mathematical sense, this means making the edges of the gamut saddle points, allowing smooth curves the pass through the hard edge, by momentarily stopping there. Per channel tone mapping is a way of doing this, but does so very extremely (causing the “notorious six”). Other tradeoffs exist in this space which more delicately balance maintaining hues and keeping the output mapping smooth.
*) Or some other luminance/brigthness/lightness-like metric
I would argue 1. isn’t really a good option. The artifacts it causes are too large and it is also computationally expensive. If being able to produce the entire gamut is a requirement, 3. is the only option left. We need to balance smoothness and hue distortions. So what can that look like?
There are certainly other ways to achieve this, but one approach is the following:
- Start by doing hue preserving gamut compression to a smooth gamut that is larger than the target RGB gamut.
- In the target RGB space, perform a soft clipping step.
The smooth gamut approximation needs to be larger by enough margin that the soft clip step reaches the hull of the gamut.
How much this mapping preserves hue and lightness depends on how close the smooth gamut approximation is to the real gamut. Here is an example with a fairly simple approximation (so, this is not the best this method could perform):
Here of course neither example is great looking, but that will always be the price for reaching the hull of an RGB gamut, the hull will never look great.
On the other hand, if backing of the hull slightly, the pure hue preserving method still shows issues around where the edges of the RGB gamut is projected, while the slightly hue distorting solution provides a much smoother result.
The code for this test is here:
And a related experiment used to derive it here:
Again, this is not the best this method could perform, it is just a quick experiment. The current gamut approximation was made to be simple enough to not require precalculating and data per RGB gamut. You with an optimization process you can definitely get a quite tight fit that is cheap to precompute (and it won’t be very expensive, just not fast enough to run per pixel).
Finding a path to white
I think it is also worthwhile to analyze a bit how and why saturation/desaturation occurs when applying tone curve per channel in RGB (and a similar but more complex process occurs in film). While per channel curves behave quite terribly for saturated colors close to its primaries, for low/moderately saturated colors they do behave quite nicely and automatically provide saturation changes that nicely match their tone curves. By analysing how this works, we can get some insight into how to generalize in a way that gets rid of the problems.
So, lets analyze this a bit mathematically. We have three linear source values: R, G and B and a tone curve f(x). If we are looking at a color with low saturation relative to the RGB primaries, all the channel will be close to some grayscale intensity I. We can then express R, G and B as
R = I + ΔR
G = I + ΔG
B = I + ΔB
Where ΔR, ΔG and ΔB are some small differences. If we apply our tone curve to this, we get:
f(R) = f(I + ΔR)
f(G) = f(I + ΔG)
f(B) = f(I + ΔB)
We can now use the property that ΔR, ΔG and ΔB are to analyze what is going on. We have that:
f(R) ≈ f(I) + ΔR f’(I)
f(G) ≈ f(I) + ΔG f’(I)
f(B) ≈ f(I) + ΔB f’(I)
where f’(x) is the derivative of the tone curve.
With this we can now see that the saturation change is primarily driven by the derivative of the tone curve, and more specifically saturation is changed by f’(x)/f(x).
Here’s an example of what this looks like for a simple test curve:
Designing a hue linear path to white
So, with this knowledge how can we design a path to white that keeps the clear relation between tone curve and desaturation but preserves hue? For this part, lets also ignore the output gamut and just look at the case where we are compressing dynamic range more freely (and then we can gamut compress the results afterwards).
Perceptual color models with good hue linearity prediction is of course part of the answer here, since we can then desaturate in straight lines in that space and maintain hue. The other question to work out is what to use for our intensity I. What we need is some sort of way to map a given color to a 1D intensity. This intensity will drive the tone curve is applied to that particular color, and how intense it needs to be to desaturate.
One possible criteria for how quickly colors should desaturate is to try and avoid the color appearing brighter than the white color we are desaturating towards. In other words, we want to avoid some intermediate color appearing to fluoresce (more technically this boundary is often referred to as g0). Or, at least it can be useful to control how much colors fluoresce on the way. There will be a balance between using the entire RGB gamut and getting vivid colors, and avoiding strange fluorescing effects.
Another option is to use something more like a regular lightness estimate or luminance, but this is problematic. Doing so results in yellows desaturating very quickly since they are considered bright, while deep blues barely desaturating at all until very bright.
So, we need some kind of metric for how close a color is to appear to fluoresce. I haven’t found detailed data or simple approximations for this easy accessible, so haven’t experimented with approximating g0 directly. A related concept though is the MacAdam limit, the theoretical limit for how bright a surface can be (without literally fluorescing, rather than appearing to fluoresce), and that is fairly easy to approximate. I set up a test for that using the excellent colour python library here to approximate it: Google Colab
With this, we now have a MacAdam limit approximation to try and use as I.
I’ve set up a little experiment using this and the gamut compression discussed here. After playing around with this, having an option to tradeoff colorfulness/fluorescence definitely makes sense, so this is something I added (in the parameter called “offset”). For anyone interested in the details, the code itself contains quite a bit more details than discussed here and at least some explaining comments.
Showing this in just a couple of images is hard, but here a few teasers of what a transform like this can look like. Here are some emissive circles using blends of rec2020 primaries transformed with an sRGB output. The first image has I set to the MacAdam limit approximation, then the offset parameters is adjusted to allow more saturated colors:
The entire experiment is here:
Here is a plot of blends of sRGB primaries through this transform (using an inbetween saturation). I’ve tried to replicate the test image circulated here a few time, but the exposure scale is probably a bit different.
This is available here:
More technical details
These experiments output sRGB and use a tone curve based on a numerical fit to the ACES rec709 tone curve. I’m definitely not saying this tone curve is the right one to use, I simply used it because it was easy to get started with and to differentiate. The matrices are a bit hard coded in this example, but it is easy to adopt this transform to other output gamuts, it is just about changing a few matrices here and there. I used the LMS matrix and non linearity of Oklab, since it is easy to work with mathematically, but the ideas don’t depend on that. Also worth noting is that I think it is possible to make an inverse transform of this fairly easily (maybe except for the current RGB soft clipping implementation, but that could be changed to somethings that inverts).
I haven’t tried this out with the test images circulating here, that would definitely be interesting to compare of course, since these artificial test images don’t say much. I did try it with some other things myself, but not yet with anything I can share.
Regarding input gamuts
I think there is one last issue worth addressing, which is the input gamut.
The gamut mapping I implemented here is able to reach all colors in the output space, but in many cases does requires inputs outside the visible gamut. This has the nice property that commonly occurring visible colors can have nice and smooth paths to white, but you can still reach bright and extremely saturated colors, by pushing the color outside the visible gamut. This is especially true for yellows more than other colors, since the difference between a single wavelength yellow and commonly occurring yellow colors is quite small, so not a lot of real colors to use.
This is not without issues though. One issue is that most (or all?) current perceptual models don’t really extrapolate gracefully outside the visible gamut, including Oklab. Another issue is that you need input outside both the visible gamut and AP0 to reach all output colors (I don’t know enough about the ACES flow overall to judge how big of an issue this is).
I can think of a few ideas to mitigate these issues, although I don’t know enough about how this would used practically to judge what is best or most feasible:
- Have a very saturated default look. This way the boundaries can be pushed into the visible range. The big drawback of course is that to achieve a natural look you will have to desaturate the input significantly before the output transform (ideally using the same perceptual model as the color space itself to not cause distortions).
- Similarly, you can have some kind of gamut uncompress step before the output transform. This could take the input color space into account, so that the for example boundary of AP1 maps to max saturation (this could then directly map to the same perceptual model as the output transform).
- Take input in a perceptual model instead and specify looks with an output in a perceptual color space. I think this makes some sense, but I’d also assume this would be very hard to do in practice.
Depending on the solution, one issue will be how the perceptual model behaves outside the visible gamut. I required I think it is very feasible to make a new model that matches current models in terms of hue linearity while having much better behavior outside the visible gamut.