Nice! Will need to add it to the notebook, not sure if we want to try maintaining parity but it could be a good idea.
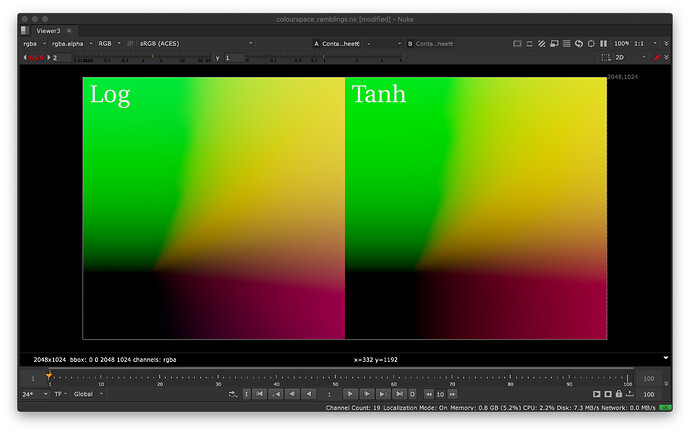
Visual inspection is certainly not enough because the eye is notoriously bad at detecting those type of low-frequency changes, where it starts being problematic is more with grading tools relying on qualifiers, here is some selective red suppression:
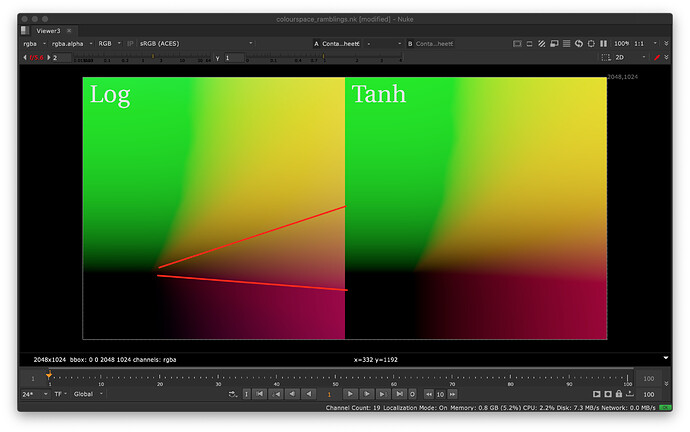
I can almost see a desaturated cone where the log variant starts kicking:
It gets worse by tweaking the distance limits. It might be a contrived example, but it is the type of things we should look for, especially because the operator will eventually be applied before grading.
set cut_paste_input [stack 0]
version 12.1 v1
push $cut_paste_input
Expression {
expr0 "x / width - 0.25"
expr1 "y / height - 0.25"
name Expression14
selected true
xpos 3004
ypos 2027
}
Group {
name GamutCompress_blink9
label "\[value method] : \[value direction]"
selected true
xpos 3004
ypos 2051
addUserKnob {20 GamutCompress}
addUserKnob {4 method t "Choose the type of distance compression function you want to use" M {log reinhard exp atan tanh}}
addUserKnob {22 reset -STARTLINE T "n = nuke.thisNode()\nknobs = \['threshold', 'cyan', 'magenta', 'yellow']\nfor k in knobs:\n n\[k].setValue(0.2)"}
addUserKnob {6 use_gpu l "use gpu" t "use gpu for blinkscript node" -STARTLINE}
use_gpu true
addUserKnob {7 threshold t "Percentage of the gamut to affect. A value of 0.2 will leave leave the core 80% of the colors within the gamut unaffected." R 0 0.2}
threshold 0.3
addUserKnob {26 distance_limit_label l " " t "Specifies the distance beyond the gamut boundary to map to the gamut boundary for each color component." T "<b>distance limit"}
addUserKnob {7 cyan t "distance limit for the R component." R 0.001 1}
cyan 0.2
addUserKnob {7 magenta t "distance limit for the G component." R 0.001 1}
magenta 0.2
addUserKnob {7 yellow t "distance limit for the B component." R 0.001 1}
yellow 0.2
addUserKnob {26 ""}
addUserKnob {4 direction M {forward inverse}}
addUserKnob {20 info_tab l Info}
addUserKnob {26 info_label l " " T "<style> a:link \{ color: #ccc \}</style>\n<font color=#ccc>\n<b>GamutCompress</b><br>\nmaps out of gamut colors back into gamut.<br><br>\n\n<b>Method</b><br>\nSpecify the tone compression curve to use when <br>\nmapping out of gamut colors into the boundary threshold.<br>\n<a href=https://www.desmos.com/calculator/hmzirlw7tj>log</a>\n<a href=https://www.desmos.com/calculator/lkhdtjbodx>reinhard</a>\n<a href=https://www.desmos.com/calculator/s2adnicmmr>exp</a>\n<a href=https://www.desmos.com/calculator/h96qmnozpo>atan</a>\n<a href=https://www.desmos.com/calculator/xiwliws24x>tanh</a>\n<br><br>\n\n<b>Threshold</b><br>\nPercentage of the gamut to affect. If threshold is 0.2, <br>\nthe inner 80% of the gamut will be unaffected and <br>\nout of gamut values will be compressed into <br>\nthe outer 20% of the gamut's color volume.<br><br>\n\n<b>Max Distance</b><br>\nPer color component control to specify what distance will be <br>\ncompressed to the gamut boundary. For example, <br>\na value of cyan=0.2 will map colors with a distance of red=1.2 from <br>\nthe achromatic axis to red=1.0, which is the gamut boundary.<br><br><br>\n\n<b>Direction</b><br>\nSpecifies whether to apply or inverse the gamut compression operation.\n<br><br>\n<a href=https://github.com/jedypod/gamut-compress>Additional Documentation</a><br><br>\n\nWritten by <a href=https://github.com/jedypod color=red>Jed Smith</a> with <a href=https://community.acescentral.com/t/rgb-saturation-gamut-mapping-approach-and-a-comp-vfx-perspective>help</a> from the <a href=https://community.acescentral.com/c/aces-development-acesnext/vwg-aces-gamut-mapping-working-group>ACES Gamut Mapping VWG</a>"}
}
Input {
inputs 0
name Input
xpos -40
ypos -10
}
AddChannels {
name AddChannels
note_font Helvetica
xpos -40
ypos 26
}
BlinkScript {
kernelSourceFile /cave/dev/github/gamut-compress/GamutCompress.cpp
recompileCount 15
ProgramGroup 1
KernelDescription "2 \"GamutCompression\" iterate pixelWise 1dcee6a45b699c1349e8387e6472366b100957bee76685a075fd9740e0ab7c08 2 \"src\" Read Point \"dst\" Write Point 6 \"threshold\" Float 1 AAAAAA== \"cyan\" Float 1 AAAAAA== \"magenta\" Float 1 AAAAAA== \"yellow\" Float 1 AAAAAA== \"method\" Int 1 AAAAAA== \"invert\" Bool 1 AA== 6 \"threshold\" 1 1 \"cyan\" 1 1 \"magenta\" 1 1 \"yellow\" 1 1 \"method\" 1 1 \"invert\" 1 1 3 \"thr\" Float 1 1 AAAAAA== \"lim\" Float 3 1 AAAAAAAAAAAAAAAAAAAAAA== \"pi\" Float 1 1 AAAAAA=="
kernelSource "kernel GamutCompression : ImageComputationKernel<ePixelWise> \{\n Image<eRead, eAccessPoint, eEdgeClamped> src;\n Image<eWrite> dst;\n\n param:\n float threshold;\n float cyan;\n float magenta;\n float yellow;\n int method; // compression method\n bool invert;\n\n local:\n float thr;\n float3 lim;\n float pi;\n\n void init() \{\n pi = 3.14159265359;\n\n // thr is the percentage of the core gamut to protect: the complement of threshold.\n thr = (1 - threshold);\n \n // lim is the max distance from the gamut boundary that will be compressed\n // 0 is a no-op, 1 will compress colors from a distance of 2.0 from achromatic to the gamut boundary\n // if method is Reinhard, use the limit as-is\n if (method == 0) \{\n lim = float3(cyan+1, magenta+1, yellow+1);\n \} else \{\n // otherwise, we have to bruteforce the value of limit \n // such that lim is the value of x where y=1 - also enforce sane ranges to avoid nans\n // importantly, this runs once at the beginning of evaluation, NOT per-pixel!!!\n lim = float3(\n bisect(max(0.0001, cyan)+1), \n bisect(max(0.0001, magenta)+1), \n bisect(max(0.0001, yellow)+1));\n \}\n \}\n\n // calculate hyperbolic tangent\n float tanh( float in) \{\n float f = exp(2.0f*in);\n return (f-1.0f) / (f+1.0f);\n \}\n\n // calculate inverse hyperbolic tangent\n float atanh( float in) \{\n return log((1.0f+in)/(1.0f-in))/2.0f;\n \}\n\n // compression function which gives the y=1 x intersect at y=0\n float f(float x, float k) \{\n if (method == 0) \{\n return k;\n \} else if (method == 1) \{\n // natural exponent compression method\n return -log((-x+1)/(thr-x))*(-thr+x)+thr-k;\n \} else if (method == 2) \{ \n // natural logarithm compression method\n return (exp((1-thr+thr*log(1-x)-x*thr*log(1-x))/(thr*(1-x))))*thr+x*thr-k;\n \} else if (method == 3) \{\n // arctangent compression method\n return (2*tan( (pi*(1-thr))/(2*(x-thr)))*(x-thr))/pi+thr-k;\n \} else if (method == 4) \{\n // hyperbolic tangent compression method\n return atanh((1-thr)/(x-thr))*(x-thr)+thr-k;\n \}\n \}\n\n int sign(float x) \{\n return x == 0 ? 0 : x > 0 ? 1 : 0;\n \}\n\n float bisect(float k) \{\n // use a simple bisection algorithm to bruteforce the root of f\n // returns an approximation of the value of limit \n // such that the compression function intersects y=1 at desired value k\n // this allows us to specify the max distance we will compress to the gamut boundary\n \n float a, b, c, y;\n float tol = 0.0001; // accuracy of estimate\n int nmax = 100; // max iterations\n\n\n // set up reasonable initial guesses for each method given output ranges of each function\n if (method == 2) \{\n // natural logarithm needs a limit between -inf (linear), and 1 (clip)\n a = -5;\n b = 0.96;\n \} else if (method == 4) \{\n // tanh needs more precision\n a = 1.000001;\n b = 5;\n \} else \{\n a = 1.0001;\n b = 5;\n \}\n\n if (sign(f(a, k)) == sign(f(b, k))) \{\n // bad estimate. return something close to linear\n if (method == 2) \{\n return -100;\n \} else \{\n return 1.999999;\n \}\n \}\n c = (a+b)/2;\n y = f(c, k);\n if (y == 0) \{\n return c; // lucky guess\n \}\n\n int n = 1;\n while ((fabs(y) > tol) && (n <= nmax)) \{\n if (sign(y) == sign(f(a, k))) \{\n a = c;\n \} else \{\n b = c;\n \}\n c = (a+b)/2;\n y = f(c, k);\n n += 1;\n \}\n return c;\n \}\n\n\n // calculate compressed distance\n float compress(float dist, float lim) \{\n float cdist;\n if (dist < thr) \{\n cdist = dist;\n \} else \{\n if (method == 0) \{\n // simple Reinhard type compression suggested by Nick Shaw and Lars Borg\n // https://community.acescentral.com/t/simplistic-gamut-mapping-approaches-in-nuke/2679/3\n // https://community.acescentral.com/t/rgb-saturation-gamut-mapping-approach-and-a-comp-vfx-perspective/2715/52\n // example plot: https://www.desmos.com/calculator/h2n8smtgkl\n if (invert == 0) \{\n cdist = thr + 1/(1/(dist - thr) + 1/(1 - thr) - 1/(lim - thr));\n \} else \{\n cdist = thr + 1/(1/(dist - thr) - 1/(1 - thr) + 1/(lim - thr));\n \}\n \} else if (method == 1) \{\n // natural exponent compression method: plot https://www.desmos.com/calculator/jf99glamuc\n if (invert == 0) \{\n cdist = lim-(lim-thr)*exp(-(((dist-thr)*((1*lim)/(lim-thr))/lim)));\n \} else \{\n cdist = -log((dist-lim)/(thr-lim))*(-thr+lim)/1+thr;\n \}\n \} else if (method == 2) \{\n // natural logarithm compression method: plot https://www.desmos.com/calculator/rv08vuzqjk\n if (invert == 0) \{\n cdist = thr*log(dist/thr-lim)-lim*thr*log(dist/thr-lim)+thr-thr*log(1-lim)+lim*thr*log(1-lim);\n \} else \{\n cdist = exp((dist-thr+thr*log(1-lim)-lim*thr*log(1-lim))/(thr*(1-lim)))*thr+lim*thr;\n \}\n \} else if (method == 3) \{\n // arctangent compression method: plot https://www.desmos.com/calculator/olmjgev3sl\n if (invert == 0) \{\n cdist = thr + (lim - thr) * 2 / pi * atan(pi/2 * (dist - thr)/(lim - thr));\n \} else \{\n cdist = thr + (lim - thr) * 2 / pi * tan(pi/2 * (dist - thr)/(lim - thr));\n \}\n \} else if (method == 4) \{\n // hyperbolic tangent compression method: plot https://www.desmos.com/calculator/sapcakq6t1\n if (invert == 0) \{\n cdist = thr + (lim - thr) * tanh( ( (dist- thr)/( lim-thr)));\n \} else \{\n cdist = thr + (lim - thr) * atanh( dist/( lim - thr) - thr/( lim - thr));\n \}\n \}\n \}\n return cdist;\n \}\n\n\n void process() \{\n // source pixels\n float3 rgb = float3(src().x, src().y, src().z);\n\n // achromatic axis \n float ach = max(rgb.x, max(rgb.y, rgb.z));\n\n // distance from the achromatic axis for each color component aka inverse rgb ratios\n // distance is normalized by achromatic, so that 1.0 is at gamut boundary, and avoiding 0 div\n float3 dist = ach == 0 ? float3(0, 0, 0) : fabs(rgb-ach)/ach; \n\n // compress distance with user controlled parameterized shaper function\n float3 cdist = float3(\n compress(dist.x, lim.x),\n compress(dist.y, lim.y),\n compress(dist.z, lim.z));\n\n // recalculate rgb from compressed distance and achromatic\n // effectively this scales each color component relative to achromatic axis by the compressed distance\n float3 crgb = ach-cdist*ach;\n\n // write to output\n dst() = float4(crgb.x, crgb.y, crgb.z, src().w);\n \}\n\};"
useGPUIfAvailable {{parent.use_gpu}}
rebuild ""
GamutCompression_threshold {{parent.threshold}}
GamutCompression_cyan {{parent.cyan}}
GamutCompression_magenta {{parent.magenta}}
GamutCompression_yellow {{parent.yellow}}
GamutCompression_method {{parent.method}}
GamutCompression_invert {{parent.direction}}
rebuild_finalise ""
name GamutCompress
selected true
xpos -40
ypos 80
}
Output {
name Output
xpos -40
ypos 134
}
end_group
HueCorrect {
hue {sat {}
lum {}
red {curve 0 0.25 1 1 1 1 0 s0}
green {}
blue {}
r_sup {}
g_sup {}
b_sup {}
sat_thrsh {}}
name HueCorrect1
selected true
xpos 3004
ypos 2083
}