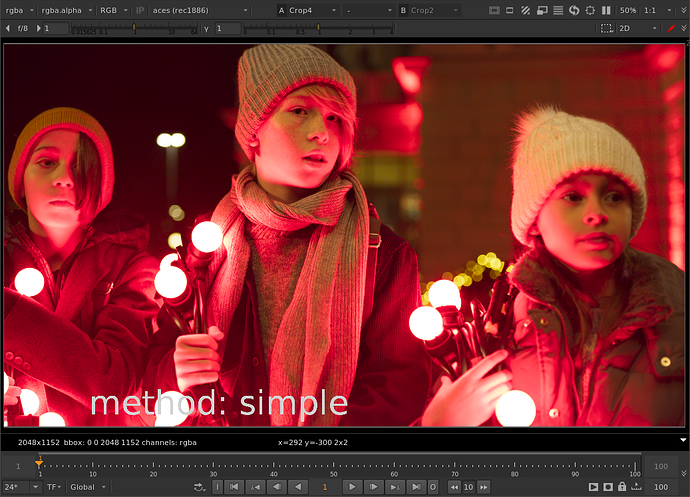
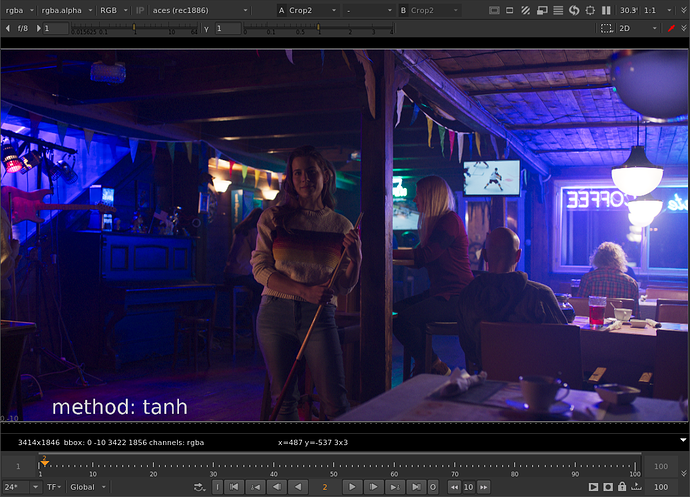
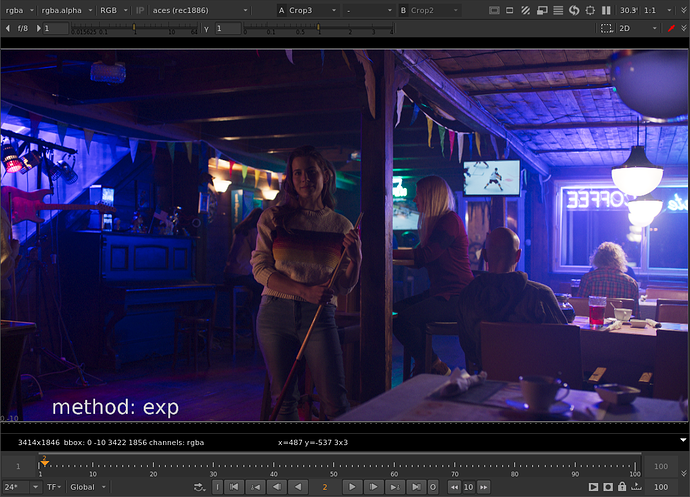
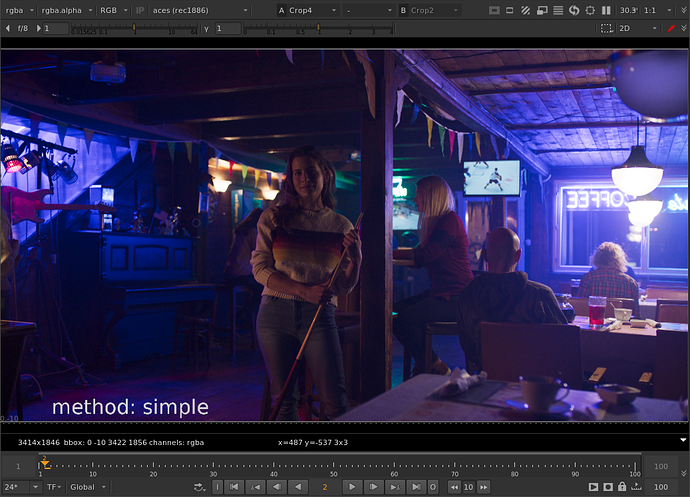
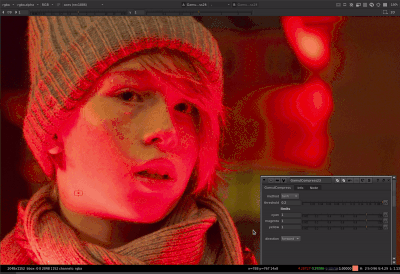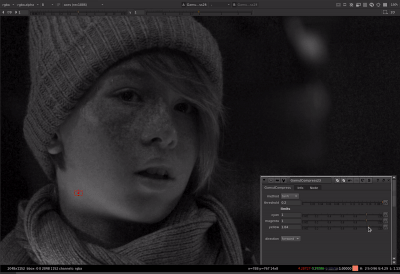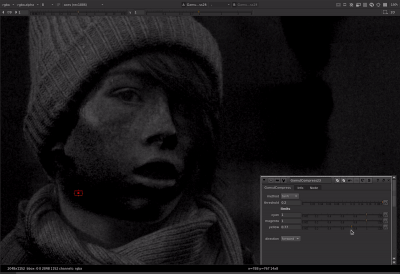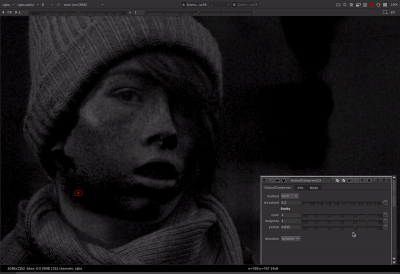
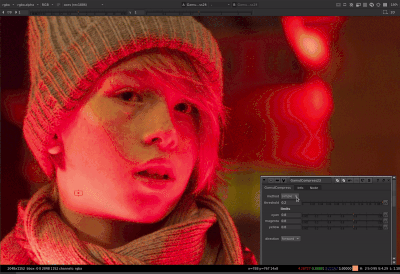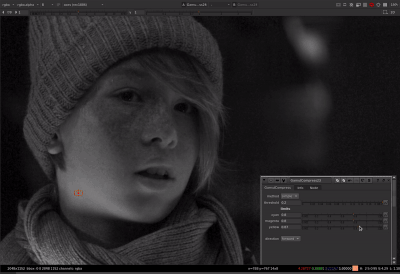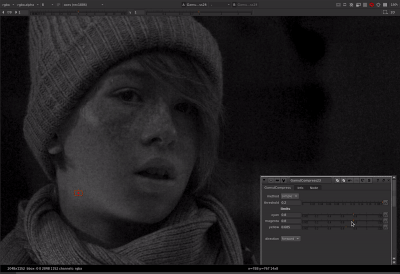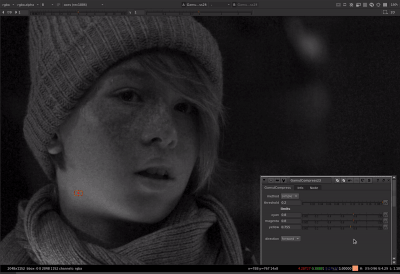
That helped me figure it out. Thanks for teaching me math @Thomas_Mansencal 
I have a few more updates. I figured out the bug with calculating the inverse. It was just a simple thing I missed. I needed to correctly inverse the calculation of the scale factor.
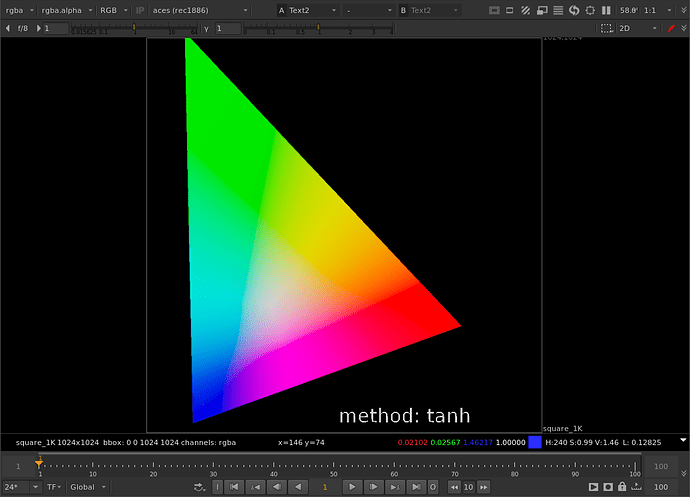
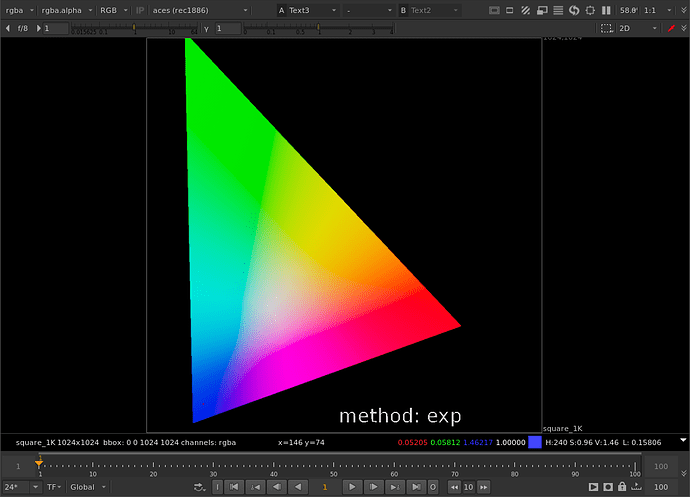
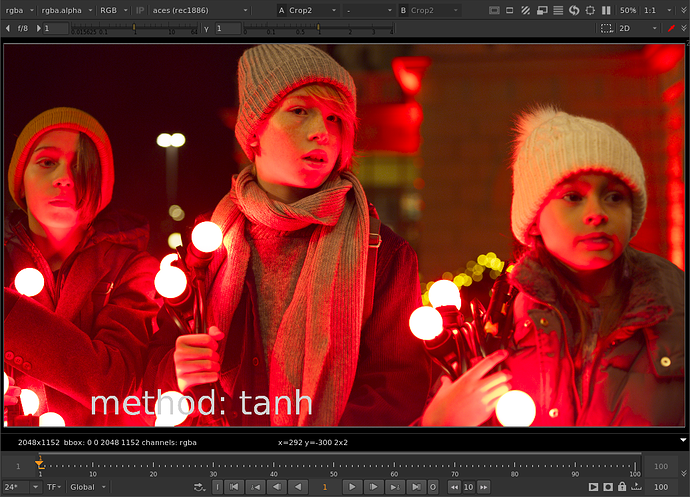
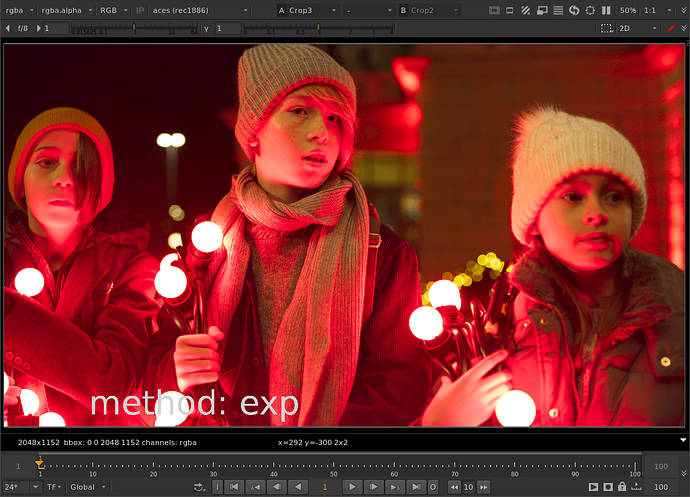
Thanks to Thomas’ help with the tanh function I was able to get the parameters to behave the same between both methods. For the limit controls of cyan, magenta, or yellow: When limit is at 0, no compression is applied. When limit is at 1, out of gamut colors are compressed to the gamut boundary. When limit is greater than 1 (with a max of 1/(1-threshold) which would be a hard clip), out of gamut colors are compressed more than the gamut boundary.
For inverting the gamut compression, there are still differences. I think it is caused by the asymptotic nature of the compression curve and a lack of precision, but it could very well be something else that I’m missing. Anyone sees something I’m not please let me know! 
I am able to get a perfect roundtrip if I use the original non-gamut compressed image to calculate the achromatic distance from… To allow this workflow I’ve added a “orig” input on the nuke node.
Updated blinkscript and nuke expression node is here:
- Nuke Blinkscript C++ Code
- Two Nuke nodes: a blinkscript node and the same thing implemented as a simple expression node
@nick Thanks for the DCTL! That should be useful. It’s pretty cool how similar CTL and C is, it’s super easy to port C code over.
As before here’s the full source for the blinkscript so it’s easy to look over:
kernel GamutCompression : ImageComputationKernel<ePixelWise> {
Image<eRead, eAccessPoint, eEdgeClamped> src;
Image<eWrite> dst;
param:
float threshold;
float cyan;
float magenta;
float yellow;
int method;
bool invert;
bool distance;
bool d_compressed;
// calc hyperbolic tangent
float tanh( float in) {
float e = 2.718281828459f;
float f = pow(e, 2*in);
return (f-1.0f) / (f+1.0f);
}
// calc inverse hyperbolic tangent
float atanh( float in) {
return log((1.0f+in)/(1.0f-in))/2.0f;
}
void process() {
// thr is the complement of threshold.
// that is: the percentage of the core gamut to protect
float thr = 1.0f - threshold;
// bias limits by color component
// range is limited to 0.00001 > lim < 1/thr
// cyan = 0: no compression
// cyan = 1: "normal" compression with limit at 1.0
// 1 > cyan < 1/thr : compress more than edge of gamut. max = hard clip (e.g., thr=0.8, max = 1.25)
float3 lim;
lim.x = 1.0f/max(0.00001f, min(1.0f/thr, cyan));
lim.y = 1.0f/max(0.00001f, min(1.0f/thr, magenta));
lim.z = 1.0f/max(0.00001f, min(1.0f/thr, yellow));
float r = src().x;
float g = src().y;
float b = src().z;
// achromatic axis
float ach = max(r, max(g, b));
// distance from the achromatic axis for each color component
float d_r = ach == 0 ? 0 : sqrt( pow(r-ach, 2.0f)) / ach;
float d_g = ach == 0 ? 0 : sqrt( pow(g-ach, 2.0f)) / ach;
float d_b = ach == 0 ? 0 : sqrt( pow(b-ach, 2.0f)) / ach;
// compress distance for each color component
float cd_r, cd_g, cd_b;
if (method == 0.0f) {
// hyperbolic tangent softclip method suggested by Thomas Mansencal here
// https://community.acescentral.com/t/simplistic-gamut-mapping-approaches-in-nuke/2679/2
// gives good results, but perhaps the curve is too asymptotic. very little color shift.
// example plot: https://www.desmos.com/calculator/jtvzbae25q
cd_r = d_r > thr ? thr + (lim.x - thr) * tanh( ( (d_r - thr)/( lim.x-thr))) : d_r;
cd_g = d_g > thr ? thr + (lim.y - thr) * tanh( ( (d_g - thr)/( lim.y-thr))) : d_g;
cd_b = d_b > thr ? thr + (lim.z - thr) * tanh( ( (d_b - thr)/( lim.z-thr))) : d_b;
if (invert == 1.0f) {
cd_r = d_r > thr ? thr + (lim.x - thr) * atanh( d_r/( lim.x - thr) - thr/( lim.x - thr)) : d_r;
cd_g = d_g > thr ? thr + (lim.y - thr) * atanh( d_g/( lim.y - thr) - thr/( lim.y - thr)) : d_g;
cd_b = d_b > thr ? thr + (lim.z - thr) * atanh( d_b/( lim.z - thr) - thr/( lim.z - thr)) : d_b;
}
} else if (method == 1.0f) {
// softclip method suggested by Nick Shaw here
// https://community.acescentral.com/t/simplistic-gamut-mapping-approaches-in-nuke/2679/3
// good results, easy to bias look with limits
// example plot: https://www.desmos.com/calculator/jyewfptd4y
cd_r = d_r > thr ? thr+(-1/((d_r-thr)/(lim.x-thr)+1)+1)*(lim.x-thr) : d_r;
cd_g = d_g > thr ? thr+(-1/((d_g-thr)/(lim.y-thr)+1)+1)*(lim.y-thr) : d_g;
cd_b = d_b > thr ? thr+(-1/((d_b-thr)/(lim.z-thr)+1)+1)*(lim.z-thr) : d_b;
if (invert == 1.0f) {
// inversed compression distance for each color component
cd_r = d_r > thr ? (pow(thr, 2.0f) - thr*d_r + (lim.x-thr)*d_r) / (thr + (lim.x-thr) - d_r) : d_r;
cd_g = d_g > thr ? (pow(thr, 2.0f) - thr*d_g + (lim.y-thr)*d_g) / (thr + (lim.y-thr) - d_g) : d_g;
cd_b = d_b > thr ? (pow(thr, 2.0f) - thr*d_b + (lim.z-thr)*d_b) / (thr + (lim.z-thr) - d_b) : d_b;
}
}
float c_r, c_g, c_b;
if (invert == 1.0f) {
// scale up each color component relative to achromatic axis by gamut uncompression factor
c_r = (r-ach)*((cd_r-d_r)+1.0f)+ach;
c_g = (g-ach)*((cd_g-d_g)+1.0f)+ach;
c_b = (b-ach)*((cd_b-d_b)+1.0f)+ach;
} else {
// scale down each color component relative to achromatic axis by gamut compression factor
c_r = (r-ach)/((d_r-cd_r)+1.0f)+ach;
c_g = (g-ach)/((d_g-cd_g)+1.0f)+ach;
c_b = (b-ach)/((d_b-cd_b)+1.0f)+ach;
}
// write to output
dst() = float4(c_r, c_g, c_b, 1);
// debug outputs
if (distance == 1.0f) {
if (d_compressed == 1.0f) {
dst() = float4(cd_r, cd_g, cd_b, 1.0f);
} else {
dst() = float4(d_r, d_g, d_b, 1.0f);
}
}
}
};
) works good for scene-referred data for a general any gamut to any gamut mapper, and it ticks all the boxes we have defined :-).
