More Tonescale Sigmoid Ramblings
The last couple weeks I’ve been doing some more explorations on this topic. I’ll summarize some of the more interesting points and thought-processes here for those rare persons who might still be following this thread.
A Tale of Two Contrasts
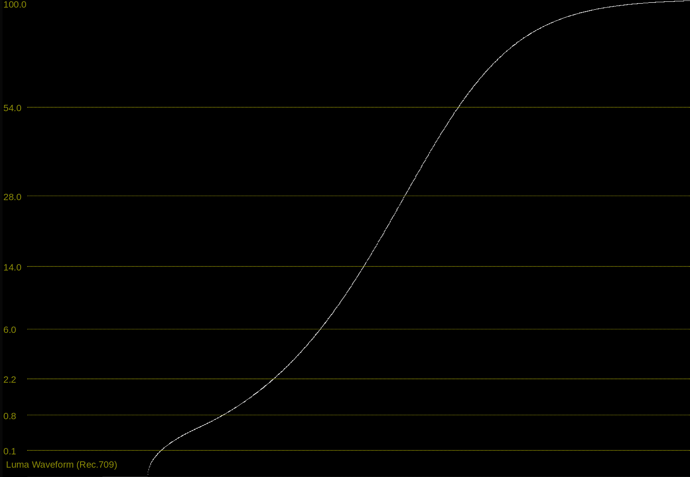
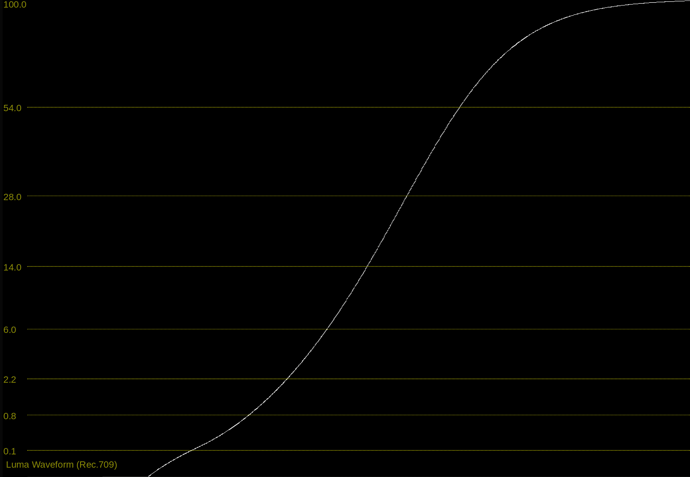
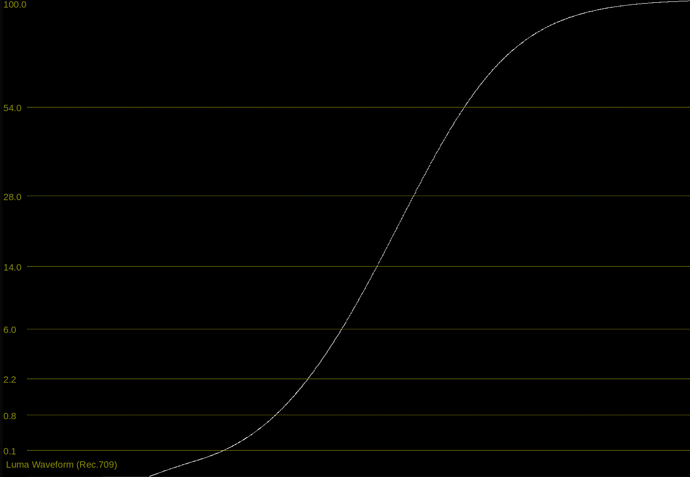
At the end of this meeting, I did a quick demo of the different behavior of contrast / exponent adjustments between these two functions
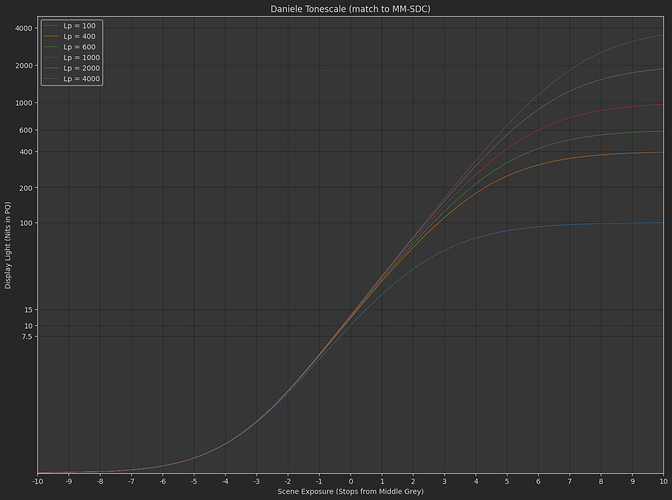
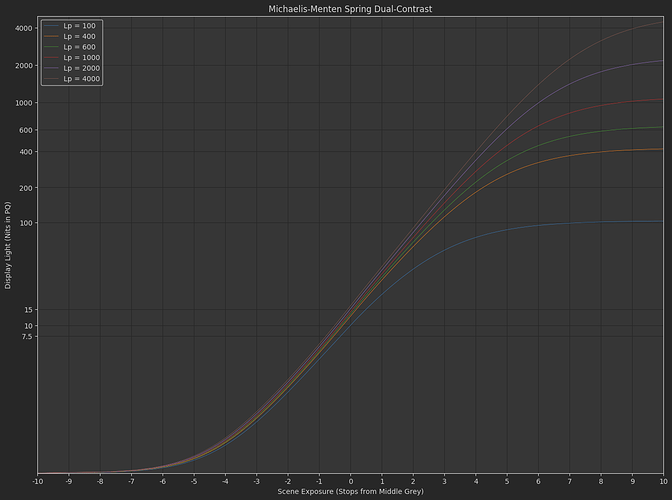
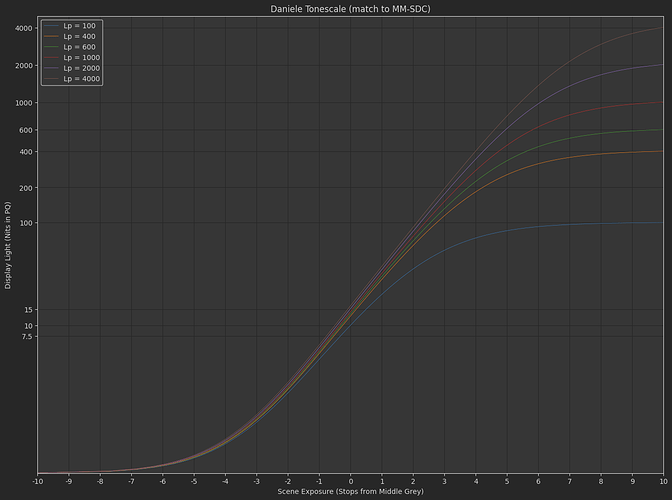
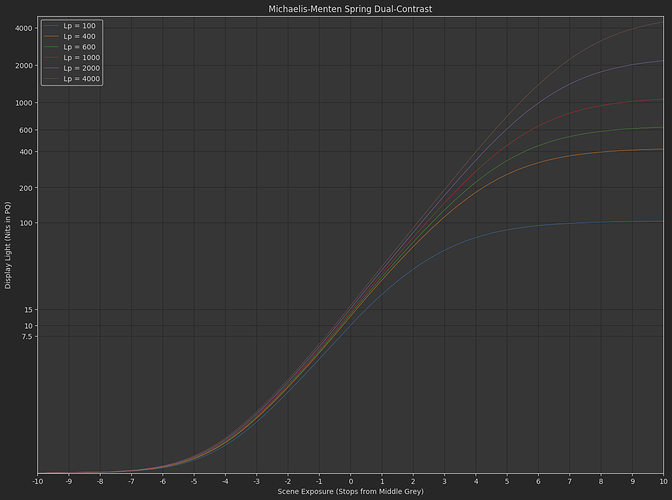
Daniele’s “Michaelis-Menten Spring Function”
f\left(x\right)=s_{1}\left(\frac{x}{s_{0}+x}\right)^{p}
where s_{0}=e_{0}s_{1}^{\frac{1}{p}} and e_{0} is the scene-linear exposure control.
the “Naka-Rushton Function” I posted before
f\left(x\right)=\frac{s_{1}x^{p}}{s_{0}+x^{p}}
The difference between the two functions is essentially where the exponent is applied.
- In Daniele’s function, contrast is adjusted as a power function in display-linear.
- In the Naka-Rushton function, contrast is adjusted as a power function in scene-linear.
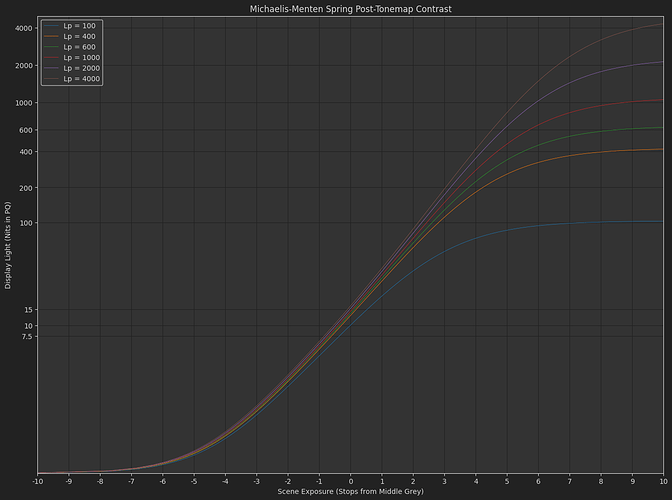
Based on all the dumb experiments I’ve done with the above two tonescale functions, it seems necessary to have more contrast in SDR than HDR. This implies the slope through middle grey changes subtly between an SDR rendering and an HDR rendering. Logically this makes sense: Since we have more dynamic range available in HDR, we would want to have less highlight compression and less stretching of mid-range values through boosted contrast. The question I’ve been exploring is how do you create a tonescale that continuously changes between SDR at 100 nits peak luminance and HDR at > 1000 nits peak luminance?
What the heck is a spring function?!
I think Daniele used this term in one of the previous meetings (or maybe I imagined it, just like I think I imagined @SeanCooper using the term “water vs balloon” to describe display gamut rendering methods). Or maybe I just have a psychological vulnerability for inventing stupid names for things.
Anyway spring just refers to a sigmoid function which can be scaled in Y without the slope through the origin changing. A simple example being f(x)=s_{1}\frac{x}{s_{1}+x}. With this function you can multiply up s_1 and the slope through the origin stays constant, while the rest of the sigmoid is scaled up vertically. This way of thinking about HDR display rendering tonescales is much more elegant and simple than the messy way I was thinking about this before.
The basic approach is to
- Set contrast with the power function
- Set “exposure” or middle grey point using the scene-linear exposure control
- Set peak white luminance using the y scale s_1.
Naka-Rushton Spring?
It’s easy to set up a “Naka-Rushton” equation in “spring” mode: f\left(x\right)=\frac{s_{1}x^{p}}{s_{0}+x^{p}}
where s_{0}\ =\frac{s_{1}}{e_{0}} and e_0 is our scene-linear scale.
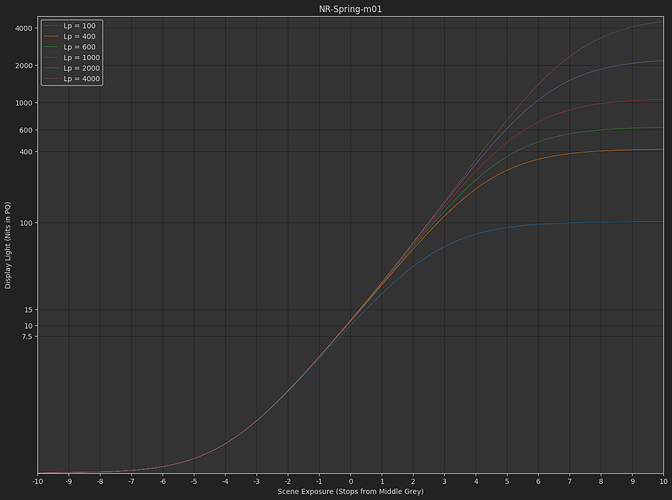
As a simple example, here is a variation on the tonescale model based on the “Naka-Rushton Tonescale Function” I posted previously. It has a constant contrast of p=1.2, constant flare compansation of f_l=0.02, and maps middle grey to 10 nits at 100 nits peak luminance.
In this model, the output y-scale is normalized so that at 100 nits peak luminance, output display-linear = 1.0, then as peak luminance increases the output peak y value increases up to 40 at 4000 nits. To normalize into a pq range where 1.0 = 10,000 nits and 0.01 = 100 nits, you would divide by 100. This makes it simple to turn on pq normalization for HDR or turn it off for SDR.
As I hinted at before, I think we would want to reduce the contrast with increasing peak luminance. With a contrast of 1.2 at 4000 nits I think the highlights are pushed too bright. Or maybe this is a problem with the tonescale function, and the reason Daniele was asking “how does it work in HDR?”
Pivoted Contrast?
After the above description of the “Naka-Rushton” function, you might be thinking
Gee if that function is just applying a power function to scene-linear input data, why not turn it into a pivoted contrast function instead, so that middle-grey isn’t shifted around when adjusting contrast?!
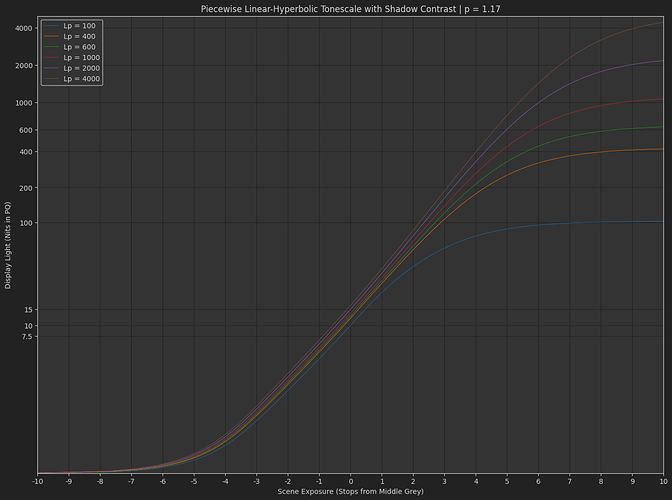
It actually seems like a valid approach using something like a 3-stage tonescale rendering:
- Scene-referred pivoted contrast adjustment (possibly with linear extension above pivot)
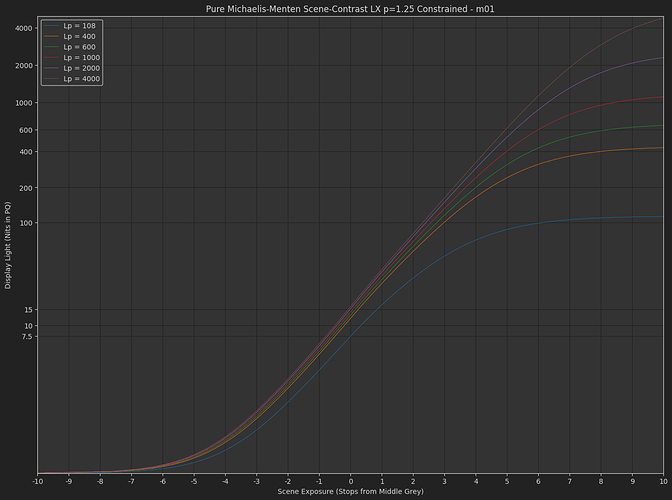
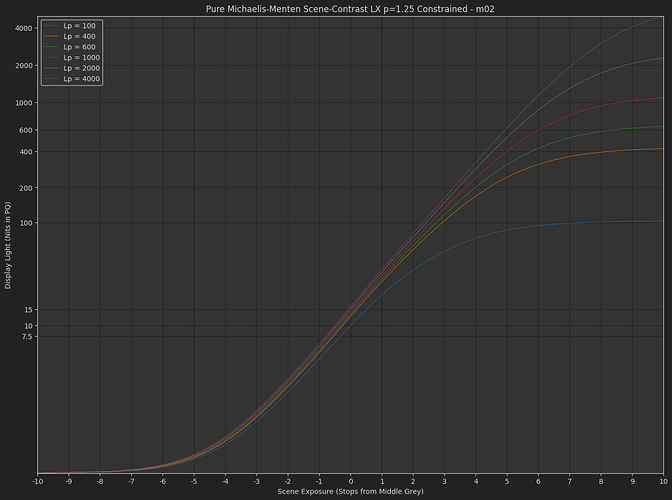
- Scene-linear to display-linear rendering using pure Michaelis-Menten function
- Flare compensation
Many Valid Approaches
Given the large quantity of garbage in my previous posts in this thread I thought it might be useful to assemble a list of tonescale functions into a single place.
In this notebook there are 3 categories of tonescale functions
- Michaelis-Menten : \frac{s_{1}x}{s_{0}+x}
Just a pure Michaelis-Menten function, no exponent, no contrast. - Michaelis-Menten
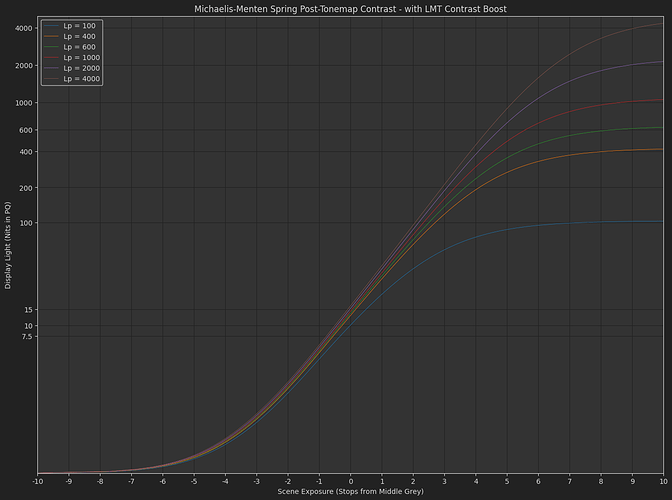
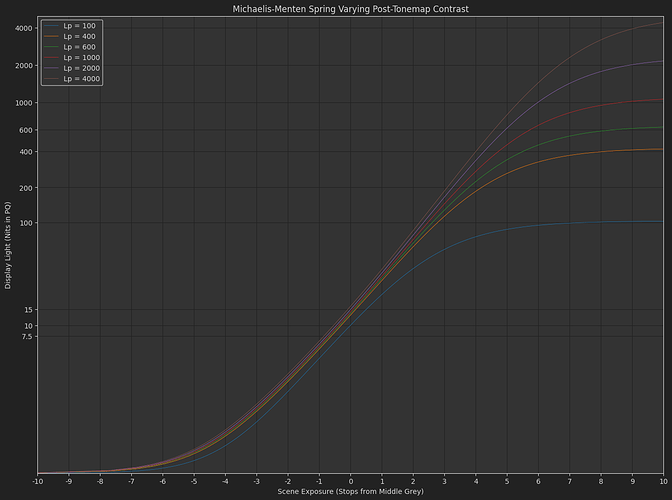
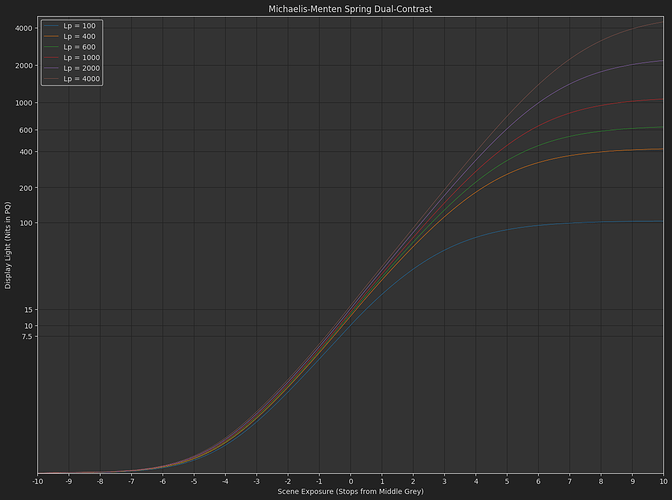
DisplayPost-Tonemap Contrast : s_{1}\left(\frac{x}{s_{0}+x}\right)^{p}
The variation Daniele posted, with exponent applied in the display-referred domain. - Michaelis-Menten
ScenePre-Tonemap Contrast : \frac{s_{1}x^{p}}{s_{0}+x^{p}}
The variation I posted above with the exponent applied in the scene-referred domain.
I have included “spring function” variations, and variations with intersection constraints where possible.
A Note on Names
Just a brief interlude to justify my decisions against @Troy_James_Sobotka 's pedantic trolling in the previous meeting.
In the original Naka-Rushton 1966 paper, the function they use is a classic Michaelis-Menten function y=s_{1}\frac{x}{x+s_{0}}. I agree that strictly speaking using this name to refer to my above function is disingenuous.
I used this name because in this other paper the “Naka-Rushton equation” is referenced as f\left(x\right)=s_{1}\frac{x^{p}}{s_{0}^{p}+x^{p}}.
Also technically speaking the function Daniele posted is a Michaelis-Menten function with an added contrast. Michaelis-Menten refers strictly to the hyperbolic function \frac{s_{1}x}{s_{0}+x}
So yeah, maybe moving forward we call these functions by what they are: The Michaelis-Menten function with contrast added in display-referred domain or scene-referred domain.